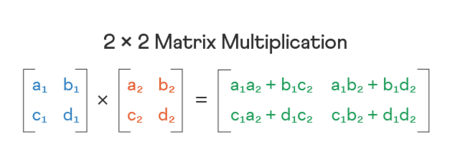Matrix Calculator

Solve Matrix Algebra: Multiplication, Inverse, and Determinants

Please enter the required details and click Calculate.

Mastering Matrix Operations

Matrices are the backbone of linear algebra, used in everything from computer graphics to economic modeling. Our Matrix Calculator supports Matrix Multiplication, Addition, Subtraction, and Transposition.

Crucially, it validates Dimensional Compatibility: for multiplication, the number of columns in Matrix A must equal the number of rows in Matrix B. If the dimensions don't match, the tool will guide you on the correct format.

How Are Matrix Calculations Performed?

Addition and subtraction are performed element-wise: $(A \pm B)_{ij} = A_{ij} \pm B_{ij}$. Determinants for $2 \times 2$ matrices use the formula $ad - bc$, while larger matrices use row reduction or expansion. Inverses are calculated via Gaussian elimination to find $A^{-1}$ such that $A \times A^{-1} = I$.2x2 Matrix Multiplication Diagram

Useful Tips 💡

  • Double-check for zero determinants if you are trying to find an inverse.
  • Matrix multiplication is NOT commutative: A \times B \neq B \times A. Order matters!

📋Steps to Calculate

  1. Set the dimensions of your matrices (Rows x Columns).

  2. Fill in the numeric elements for each matrix.

  3. Select the operation (e.g., A \times B or det(A)) and click "Calculate".

Mistakes to Avoid ⚠️

  1. Multiplying matrices in the wrong order - AB ≠ BA.
  2. Forgetting that dimensions must match for multiplication (columns A = rows B).
  3. Entering transposed matrix by mistake.
  4. Thinking determinant exists for non-square matrices.

Practical Applications📊

  1. Solve linear equations in algebra using matrix operations.

  2. Analyze data transformations in computer graphics.

  3. Optimize engineering systems with matrix calculations.

Questions and Answers

What is a matrix calculator?

A matrix operations calculator is one type of application that supports performing basic or advanced operations like multiplication, addition, subtraction, finding determinants or even inverses of structures called matrices. Such tools are greatly helpful when dealing with complex calculations involving many steps.

How to perform matrix multiplication?

To do matrix multiplication, the columns for the first matrix must equal the rows for the second matrix. Once the values are entered into the matrix multiplication calculator, use the row-by-column sum-product method to compute the product of the two matrices.

What is a determinant calculator used for?

Determinant tools are used specifically to compute the scalar quantity corresponding to certain square arrays which is essential in solving systems with several linear equations or understanding whether given matrices can be inverted (transpose). This field of study deals mostly with linear algebra.

How does the online matrix calculator compute results?

The calculator performs computations based on standard linear algebra. For matrix multiplication: $C_{ij} = \sum (A_{ik} \times B_{kj})$. For a $2 \times 2$ determinant: $\det(A) = ad - bc$. Inverses are found using Gaussian elimination or the adjugate method.

What is an inverse matrix calculator used for?

It computes $A^{-1}$, where $A \times A^{-1} = I$ (the identity matrix). This is crucial for solving systems of equations where $X = A^{-1}B$.

How do I multiply two matrices?

You multiply the elements of the rows of the first matrix by the elements of the columns of the second and sum them up. Our tool automates this tedious process.

What is the Transpose of a matrix?

The transpose (A^T) is formed by turning all the rows of the original matrix into columns and vice versa.

🔢Try More Calculators

Trigonometry Calculator
Logarithm Calculator
Circle Calculator
Disclaimer: This calculator is designed to provide helpful estimates for informational purposes. While we strive for accuracy, financial (or medical) results can vary based on local laws and individual circumstances. We recommend consulting with a professional advisor for critical decisions.