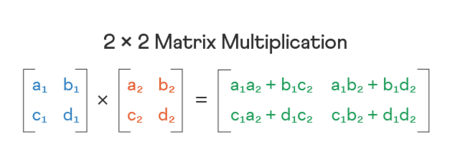Matris Hesap Makinesi

Matris Hesaplama ile Çarpma ve Determinantı Hızlı Çözün.

Lütfen gerekli detayları girin ve Hesapla'ya tıklayın.

Hesaplama Örnekleri

Hesaplama Durumu Sonuç
2x2 Matrisin determinantı [[4,1],[3,2]] 5
İki matrisin çarpımı Yeni sonuç matrisi
Bir matrisin tersini (inverse) bulma A⁻¹ hesaplaması

Matris Hesap Makinesi Nasıl Kullanılır?

Temel matris hesap makinesini kullanırken, gerekli işlemi (iki matris çarpımı, çıkarma, toplama) seçtiğinizden emin olun. Matrislerin boyutlarını girerken, çarpma için ilk matrisin sütun sayısının ikinci matrisin satır sayısına eşit olması gibi uyumluluk ön koşullarını göz önünde bulundurun. Her matris elemanının sayısal değerlerini uygun kutulara girin ve değerlerin doğru olduğundan emin olun. Girişleri doğruladıktan sonra “Hesapla”ya tıklayın. Çıktı, seçilen işleme bağlı olarak skaler bir değer veya matris gösterecektir. Ters matris veya determinant gibi daha karmaşık hesaplamalar için adım adım çözüm sunulur, böylece anlayışınız artar. Hatalardan kaçınmak için minimum gerekli doğru boyutları ve boolean değer girişlerini her zaman doğrulayın.

Matris Hesaplamaları Nasıl Yapılır?

Her işlem, türüne bağlı olarak farklı şekilde gerçekleştirilir. Toplama ve çıkarma işlemleri eleman bazında yapılır, ancak aynı boyutlu matrisler gerektirir. 2x2 ve 3x3 matrisler için determinantlar standart formülle hesaplanırken, daha büyük matrisler için satır indirgeme yöntemi uygulanır. Ters matris, Gauss eleme yöntemi veya adjugat yöntemleriyle hesaplanır ve gerektiğinde bu formüller uygulanır. Türkiye'de mühendislik eğitiminde matris çarpma hesaplama, robotik sistemlerde dönüşümleri modellemek için kullanılır; örneğin, bir 2x2 matrisin determinantını bulmak koordinat değişimlerini sağlar. Matris toplama çıkarma veya matris tersini alma yöntemleriyle, ekonomi modellerinde veri analizi kolaylaşır, örneğin üretim matrisleri. Lineer cebir uygulamaları olarak, bilgisayar grafiğinde görüntü dönüşümleri de desteklenir.2x2 Matris Çarpımı Diyagramı

Uzman Tavsiyeleri 💡

  • Matris elemanlarını doğru sırayla girin.
  • İşlemlerden önce matris boyutlarını kontrol edin.

📋Hesaplama Adımları

  1. Sağlanan seçeneklerden istenen işlemi seçin.

  2. Her matrisin doğru değerlerini ve boyutlarını girin.

  3. Hesaplanmış sonuçları almak için “Hesapla”ya basın.

Kaçınılması Gereken Hatalar ⚠️

  1. Boyutları uyumlu olmayan iki matrisi çarpmaya çalışmak.
  2. Çarpma sırasına dikkat etmemek (A x B matrisi, B x A matrisine eşit değildir).
  3. Determinant veya ters matris hesaplarken işaret hatası yapmak.
  4. Veri girerken satırları (yatay) ve sütunları (dikey) karıştırmak.

Pratik Uygulamalar📊

  1. Lineer cebirde matris işlemlerini kullanarak denklemleri çözün.

  2. Bilgisayar grafiklerinde veri dönüşümlerini analiz edin.

  3. Mühendislik sistemlerini matris hesaplamalarıyla optimize edin.

Sıkça Sorulan Sorular (SSS)

Matris hesap makinesi nedir?

Matris işlemleri hesap makinesi, çarpma, toplama, çıkarma, determinant bulma veya matrislerin tersini alma gibi temel veya ileri işlemleri destekleyen bir uygulamadır. Çok adımlı karmaşık hesaplamalarla uğraşırken bu tür araçlar oldukça yardımcıdır.

Matris çarpımı nasıl yapılır?

Matris çarpımı yapmak için, ilk matrisin sütun sayısı ikinci matrisin satır sayısına eşit olmalıdır. Değerleri matris çarpma hesap makinesine girdikten sonra, satır-sütun toplam-çarpım yöntemi kullanılarak iki matrisin çarpımı hesaplanır.

Determinant hesaplama ne için kullanılır?

Determinant hesaplama, kare dizilerin skaler değerini bulur, lineer denklemleri çözmek veya ters matris alınabilirliğini anlamak için kullanılır.

3x3 diziler için lineer cebir aracı kullanılabilir mi?

Evet, 3x3 diziler için ters, determinant ve çarpım hesaplamaları yapar, değerleri girin ve doğru sonuçlar alın.

Çevrimiçi lineer cebir aracı nasıl çalışır?

Standart lineer cebir denklemleriyle çalışır: çarpım için C[i,j] = Σ(A[i,k] * B[k,j]), 2x3 determinant için ad - bc, 3x3 için satır genişletme, ters için Gauss eleme kullanılır, matematiksel standartlarla doğrulanmıştır.

Ters matris hesaplama ne için kullanılır?

Ters matris aracı, kare dizinin tersini ($A^{-1}$) hesaplar, lineer denklemleri çözmek veya mühendislikte dönüşümleri analiz etmek için önemlidir.

Transpoz matris nasıl türetilir?

Satır ve sütunları değiştirerek transpoz hesaplanır, lineer cebir aracı boyut ve değerlerle anında transpoz ($A^T$) sunar, veri analizi için faydalıdır.

🔢Daha Fazla Hesap Makinesi Deneyin

Trigonometri Hesaplama Aracı
Logaritma Hesaplayıcısı
Çember Hesaplayıcı
Not: Bu hesaplayıcı, bilgilendirme amaçlı faydalı tahminler sunmak için tasarlanmıştır. Doğruluk için çaba göstersek de sonuçlar yerel yasalara ve bireysel durumlara göre değişiklik gösterebilir. Önemli kararlar için profesyonel bir danışmana başvurmanızı öneririz.