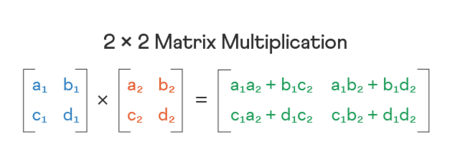Kalkulator Matriks Online

Solusi Cepat untuk Operasi Matriks dan Aljabar Linier.

Silakan masukkan detail yang diperlukan dan klik Hitung.

Contoh Perhitungan

Kasus Perhitungan Hasil
Determinan matriks 2x2 [[4,1],[3,2]] 5
Perkalian matriks A dan matriks B Hasil matriks baru
Invers matriks untuk penyelesaian persamaan linier Matriks A⁻¹

Cara Mengoperasikan Kalkulator Matriks

Pilih operasi yang Anda butuhkan: Penjumlahan, Perkalian, Determinan, atau Invers. Masukkan angka-angka ke dalam sel matriks yang tersedia.

Penting untuk diingat bahwa untuk perkalian matriks, jumlah kolom pada matriks pertama harus sama dengan jumlah baris pada matriks kedua. Alat ini sangat membantu mahasiswa di universitas Indonesia seperti UI, ITB, atau UGM dalam memverifikasi jawaban tugas Matematika Teknik atau Aljabar Linier.

Bagaimana Perhitungan Matriks Dilakukan?

Cara setiap operasi dilakukan tergantung langsung pada setiap operasi unik. Penjumlahan dan pengurangan juga dilakukan secara elemen tetapi memerlukan matriks berdimensi sama. Determinan untuk matriks 2x2 dan 3x3 menerapkan rumus standar sementara metode reduksi baris diterapkan pada matriks yang lebih besar. Invers melalui eliminasi Gaussian atau metode adjugate memberikan hasil dengan menerapkan rumus-rumus ini bila diperlukan.Diagram Perkalian Matriks 2x2

Tips & Informasi 💡

  • Pastikan tidak ada sel yang kosong; isi dengan 0 jika elemen tersebut bernilai nol.
  • Periksa kembali tanda negatif (-) pada angka sebelum menghitung.

📋Langkah Menghitung

  1. Pilih operasi yang diinginkan dari opsi yang disediakan.

  2. Masukkan nilai dan dimensi matriks yang benar.

  3. Tekan "Hitung" untuk mendapatkan hasil yang dihitung.

Kesalahan yang Harus Dihindari ⚠️

  1. Mencoba mengalikan dua matriks yang jumlah kolom dan barisnya tidak sesuai.
  2. Salah urutan saat perkalian matriks (A × B tidak sama dengan B × A).
  3. Kesalahan tanda plus/minus saat menghitung determinan atau invers.
  4. Tertukar antara baris (horizontal) dan kolom (vertikal) saat memasukkan data.

Aplikasi Praktis📊

  1. Selesaikan persamaan linier dalam aljabar menggunakan operasi matriks.

  2. Analisis transformasi data dalam grafis komputer.

  3. Optimalkan sistem teknik dengan perhitungan matriks.

Pertanyaan Seputar Layanan Kami

Apa itu kalkulator matriks?

Kalkulator operasi matriks adalah jenis aplikasi yang mendukung pelaksanaan operasi dasar atau lanjutan seperti perkalian, penjumlahan, pengurangan, menemukan determinan, atau bahkan invers dari struktur yang disebut matriks. Alat seperti ini sangat membantu saat menangani perhitungan kompleks yang melibatkan banyak langkah.

Bagaimana cara melakukan perkalian array?

Untuk perkalian array, jumlah kolom matriks pertama harus sama dengan jumlah baris matriks kedua. Masukkan nilai ke penghitung perkalian array untuk hasil produk baris-demi-kolom.

Untuk apa penghitung determinan digunakan?

Penghitung determinan menghitung skalar array persegi, penting untuk menyelesaikan persamaan linier atau memeriksa inversibilitas matrik dalam aljabar linier.

Bagaimana penghitung array online menghitung hasil?

Penghitung array menggunakan persamaan aljabar linier: perkalian C[i,j] = Σ(A[i,k] * B[k,j]), determinan (ad - bc untuk 2x2, ekspansi baris/kolom untuk 3x3), invers dengan eliminasi Gaussian.

Apa syarat dua matriks bisa dikalikan?

Jumlah kolom matriks A harus sama dengan jumlah baris matriks B.

Bagaimana cara menghitung determinan 2x2?

Gunakan rumus (ad - bc), di mana a, b, c, d adalah elemen matriks tersebut.

Apa itu matriks identitas?

Matriks persegi yang elemen diagonal utamanya adalah 1 dan elemen lainnya adalah 0.

Bagaimana alat hitung array membantu pelajar di Indonesia?

Pelajar di Indonesia, seperti di universitas teknik, dapat menggunakan penghitung array untuk menyelesaikan tugas aljabar linier seperti determinan atau invers dengan cepat.

🔢Rekomendasi Kalkulator Lainnya

Kalkulator Trigonometri
Kalkulator Logaritma
Kalkulator Lingkaran
Catatan: Kalkulator ini dirancang untuk memberikan estimasi yang bermanfaat untuk tujuan informasi. Meskipun kami mengupayakan akurasi, hasil dapat bervariasi berdasarkan hukum setempat dan keadaan individu. Kami menyarankan untuk berkonsultasi dengan penasihat profesional untuk keputusan penting.