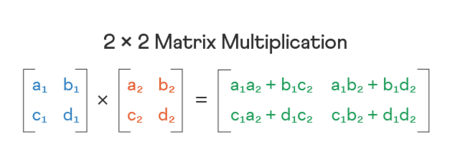Calcolatore di Matrici
Esegui Operazioni di Matrici, Determinanti e Inversi con Precisione.
📋Come Utilizzare il Calcolatore di Matrici?
-
Scegli l’operazione desiderata dalle opzioni fornite.
-
Inserisci i valori e le dimensioni corrette di ogni matrice.
-
Premi "Calcola" per ottenere i risultati calcolati.
Quando utilizzi il calcolatore di matrici elementari, assicurati di selezionare l’operazione richiesta (moltiplicazione di due matrici, sottrazione, addizione). Inserisci le dimensioni tenendo presente i prerequisiti di compatibilità, come per la moltiplicazione il numero di colonne della prima matrice deve essere uguale al numero di righe della seconda matrice. Fornisci i dati numerici per ogni valore degli elementi della matrice nelle caselle appropriate e verifica che i valori siano corretti. Clicca su “Calcola” dopo aver verificato gli input. L’output mostrerà un valore scalare risultante o una matrice a seconda dell’operazione selezionata. Viene fornita una soluzione passo-passo per calcoli più complessi come inversi o determinanti per migliorare la comprensione. Verifica sempre le dimensioni minime richieste e i valori booleani inseriti per evitare errori.
Suggerimenti utili💡
-
Inserisci gli elementi della matrice nell’ordine corretto.
-
Controlla le dimensioni della matrice prima di eseguire operazioni.
Come Vengono Eseguite le Calcolazioni di Matrici?
Il modo in cui ogni operazione viene eseguita dipende direttamente da ogni operazione unica. L’addizione e la sottrazione vengono eseguite elemento per elemento, ma richiedono matrici di dimensioni identiche. I determinanti per matrici 2x2 e 3x3 utilizzano la formula standard, mentre il metodo di riduzione delle righe viene applicato a matrici più grandi. L’inverso tramite eliminazione gaussiana o metodi di aggiunta fornisce un risultato applicando queste formule quando necessario.
Applicazioni Pratiche📊
-
Risolvi equazioni lineari in algebra utilizzando operazioni di matrici.
-
Analizza trasformazioni di dati nella grafica computerizzata.
-
Ottimizza sistemi ingegneristici con calcoli di matrici.
Domande e Risposte
Cos’è un calcolatore di matrici?
Un calcolatore di operazioni di matrici è un tipo di applicazione che supporta l’esecuzione di operazioni di base o avanzate come moltiplicazione, addizione, sottrazione, calcolo di determinanti o inversi di strutture chiamate matrici. Tali strumenti sono estremamente utili per affrontare calcoli complessi che coinvolgono molti passaggi.
Come eseguire la moltiplicazione di matrici?
Per eseguire la moltiplicazione di matrici, le colonne della prima matrice devono essere uguali alle righe della seconda matrice. Una volta inseriti i valori nel calcolatore di moltiplicazione di matrici, utilizza il metodo della somma-prodotto riga-per-colonna per calcolare il prodotto delle due matrici.
A cosa serve un calcolatore di determinanti?
I calcolatori di determinanti sono utilizzati specificamente per calcolare la quantità scalare corrispondente a determinati array quadrati, essenziale per risolvere sistemi con diverse equazioni lineari o per capire se le matrici date possono essere invertite (trasposte). Questo campo di studio riguarda principalmente l’algebra lineare.
Posso usare un risolutore di matrici per matrici 3x3?
Sì. Un calcolatore di moltiplicazione di matrici può lavorare con matrici 3x3 per ottenere inversi, calcolare determinanti e moltiplicare matrici. Inserisci semplicemente i valori della matrice e il tuo calcolatore eseguirà tutti i calcoli con precisione.
Come calcola i risultati il calcolatore di matrici online?
Il calcolatore di matrici esegue tutti i calcoli basati su equazioni standard di algebra lineare. Ad esempio, C[i,j] = Σ(A[i,k] * B[k,j]) è il modo in cui viene calcolata la moltiplicazione di matrici con matrici di input: A e B. I determinanti sono calcolati utilizzando ad - bc per matrici 2x2, e puoi espandere lungo una riga o colonna per matrici 3x3. Gli inversi utilizzano l’eliminazione gaussiana. Queste equazioni sono state verificate secondo standard matematici, quindi i risultati saranno accurati.
A cosa serve un calcolatore di matrici inverse?
Un calcolatore di matrici inverse calcola l’inverso di una matrice quadrata, indicato come $A^{-1}$, dove $A \times A^{-1} = I$ (matrice identità). È cruciale per risolvere sistemi di equazioni lineari, trasformare coordinate e analizzare trasformazioni lineari in campi come la fisica e l’ingegneria. Inserisci i valori della matrice, assicurati che sia quadrata e invertibile (determinante non zero), e lo strumento calcola l’inverso utilizzando metodi come l’eliminazione gaussiana.
Come derivare matrici trasposte da una data?
Per trovare la trasposta di una matrice, puoi utilizzare un calcolatore di matrici trasposte per scambiare le righe e le colonne della matrice, riflettendo la matrice sulla sua diagonale, trasformando le colonne in righe e viceversa. Per una matrice $ A $ con voci individuali $ a_{i,j} $, la trasposta $ A^T $ ha le voci $ a_{j,i} $. Dopo aver inserito la dimensione e i valori della matrice, la matrice trasposta risultante viene mostrata istantaneamente. Questo completa e supporta l’analisi dei dati, l’apprendimento automatico e le applicazioni di algebra lineare.
Il Calcolatore di Matrici è utile per gli studenti universitari italiani?
Per gli studenti universitari italiani che studiano algebra lineare o ingegneria, il calcolatore semplifica la risoluzione di sistemi di equazioni e trasformazioni, comuni nei corsi di matematica avanzata.
Come usare il Calcolatore di Matrici per progetti di grafica in Italia?
In Italia, dove la grafica computerizzata è utilizzata nel design e nei videogiochi, usa il calcolatore per eseguire trasformazioni di matrici, come rotazioni o scaling, per progetti creativi.