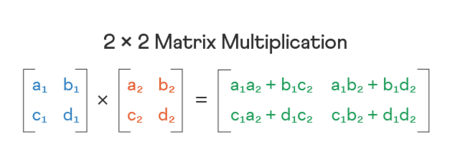Calculadora de Matrizes

Calcule Matrizes Online para Álgebra Linear e Engenharia.

Insira os detalhes necessários e clique em Calcular.

Exemplos de Cálculo

Caso de Cálculo Resultado
Determinante de matriz 2x2 ad - bc
Multiplicação A × B Nova matriz C
Matriz identidade Diagonal de 1s

Como Usar a Calculadora de Matrizes?

Primeiro, selecione a operação desejada: adição, subtração, multiplicação, determinante ou inversa. Defina as dimensões das matrizes (linhas e colunas). Insira os valores numéricos em cada célula correspondente e clique em Calcular. A ferramenta validará se as matrizes são compatíveis para a operação escolhida (por exemplo, na multiplicação, o número de colunas da matriz A deve ser igual ao número de linhas da matriz B).

Como São Realizados os Cálculos de Matrizes?

As operações com matrizes seguem regras rigorosas da álgebra linear. A adição e subtração ocorrem elemento a elemento entre matrizes de mesma dimensão. Na multiplicação, cada elemento da matriz resultante é o produto escalar de uma linha da primeira matriz por uma coluna da segunda.

Para cálculos de determinantes e inversas, utilizamos métodos como a Eliminação de Gauss e a Regra de Sarrus. Se o determinante for zero, a matriz é considerada singular e não possui inversa.

Diagrama de Multiplicação de Matrizes 2x2

Dicas Úteis 💡

  • Insira os elementos da matriz na ordem correta.
  • Verifique as dimensões da matriz antes de realizar operações.

📋Passos para Calcular

  1. Escolha a operação desejada entre as opções fornecidas.

  2. Insira os valores e dimensões corretos de cada matriz.

  3. Pressione "Calcular" para obter os resultados computados.

Erros a evitar ⚠️

  1. Tentar multiplicar matrizes cujas dimensões não são compatíveis.
  2. Não respeitar a ordem da multiplicação (A x B não é igual a B x A).
  3. Cometer erros de sinal ao calcular o determinante ou a matriz inversa.
  4. Confundir linhas (horizontais) com colunas (verticais) ao inserir os dados.

Aplicações Práticas📊

  1. Resolva equações lineares em álgebra usando operações com matrizes.

  2. Analise transformações de dados em gráficos de computador.

  3. Otimize sistemas de engenharia com cálculos de matrizes.

Perguntas e Respostas

O que é uma calculadora de matriz?

Uma calculadora de operações de matriz é um tipo de aplicação que suporta a realização de operações básicas ou avançadas como multiplicação, adição, subtração, encontrar determinantes ou mesmo inversas de estruturas chamadas matrizes. Tais ferramentas são extremamente úteis ao lidar com cálculos complexos envolvendo muitos passos.

Como realizar multiplicação de matriz?

Para fazer multiplicação de matriz, as colunas da primeira matriz devem igualar as linhas da segunda matriz. Uma vez que os valores sejam inseridos na calculadora de multiplicação de matriz, use o método de soma-produto linha-por-coluna para computar o produto das duas matrizes.

Para que serve uma calculadora de determinante?

Ferramentas de determinante são usadas especificamente para computar a quantidade escalar correspondente a certas arrays quadradas, essencial em resolver sistemas com várias equações lineares ou entender se matrizes dadas podem ser invertidas (transpostas). Esse campo de estudo lida principalmente com álgebra linear.

Posso usar um resolvedor de matriz para matrizes 3x3?

Sim. Uma calculadora de multiplicação de matriz pode trabalhar com matrizes 3x3 para obter inversas, computar determinantes e multiplicar matrizes. Basta submeter os valores da matriz e nossa ferramenta fará todos os cálculos com precisão.

Como a calculadora de matriz online computa resultados?

Utilizamos algoritmos baseados em equações padrão. Para multiplicação: C[i,j] = soma de (A[i,k] * B[k,j]). Para inversas, aplicamos o método de Gauss-Jordan, garantindo que o resultado seja matematicamente exato.

Para que serve uma calculadora de matriz inversa?

A matriz inversa (denotada como A elevado a -1) é usada para "dividir" matrizes. Ela é crucial para isolar variáveis em equações matriciais do tipo Ax = B, muito comuns em física e economia.

Como derivar matrizes transpostas?

A transposição é o processo de trocar linhas por colunas. Se o elemento a(i,j) está na linha i e coluna j, na matriz transposta ele estará na linha j e coluna i. Nossa ferramenta faz essa inversão instantaneamente.

Como as matrizes são usadas em modelagem econômica no Brasil?

No Brasil, economistas utilizam matrizes de Insumo-Produto para analisar como diferentes setores da economia (como agroindústria e serviços) interagem e dependem uns dos outros, baseando-se em dados do IBGE.

🔢Experimente Mais Calculadoras

Calculadora de Trigonometria
Calculadora de Logaritmos
Calculadora de Círculo
Nota: Esta calculadora foi projetada para fornecer estimativas úteis para fins informativos. Embora nos esforcemos pela precisão, os resultados podem variar com base nas leis locais e circunstâncias individuais. Recomendamos consultar um consultor profissional para decisões críticas.