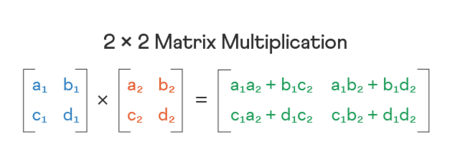Máy Tính Ma Trận

Tính Nhân, Định Thức Ma Trận Nhanh và Chính Xác.

Vui lòng nhập các chi tiết cần thiết và nhấp vào Tính toán.

Ví dụ tính toán

Trường hợp tính toán Kết quả
Tìm định thức của ma trận 2x2 [[5, 3], [2, 4]] 14
Nhân ma trận A(2x3) với ma trận B(3x2) Ma trận kết quả 2x2
Tìm ma trận nghịch đảo Ma trận A⁻¹

Cách sử dụng Máy tính Ma trận?

Khi sử dụng máy tính ma trận trực tuyến, trước tiên bạn cần chọn phép toán mong muốn như nhân hai ma trận, tính định thức hoặc tìm ma trận nghịch đảo. Nhập kích thước (số hàng và số cột) của ma trận. Hãy lưu ý điều kiện tương thích: đối với phép nhân, số cột của ma trận A phải bằng số hàng của ma trận B. Sau đó, điền các giá trị số vào từng ô tương ứng và nhấn Tính toán. Hệ thống sẽ hiển thị kết quả tức thì cùng với các bước giải chi tiết cho các phép toán phức tạp, giúp bạn dễ dàng đối chiếu và học tập.

Các Phép tính Ma trận được thực hiện như thế nào?

Mỗi phép toán ma trận tuân thủ các quy tắc đại số tuyến tính nghiêm ngặt. Phép cộng và trừ yêu cầu hai ma trận cùng kích thước, thực hiện cộng/trừ các phần tử tại cùng vị trí. Phép nhân ma trận sử dụng quy tắc Hàng nhân Cột. Định thức của ma trận 2x2 được tính theo công thức ad - bc, trong khi ma trận 3x3 và lớn hơn sử dụng phương pháp khai triển cofactor hoặc khử Gauss. Đối với ma trận nghịch đảo, chúng tôi áp dụng phương pháp Gauss-Jordan hoặc ma trận phụ hợp để tìm kết quả cuối cùng.Biểu đồ Nhân Ma trận 2x2

Mẹo hữu ích 💡

  • Nhập các phần tử ma trận theo đúng thứ tự.
  • Kiểm tra kích thước ma trận trước khi thực hiện các phép toán.

📋Các bước tính toán

  1. Chọn phép toán mong muốn từ các tùy chọn được cung cấp.

  2. Nhập các giá trị và kích thước chính xác của mỗi ma trận.

  3. Nhấn "Tính toán" để nhận kết quả đã tính toán.

Những lỗi cần tránh ⚠️

  1. Cố gắng nhân hai ma trận có kích thước không tương thích.
  2. Không tuân thủ thứ tự phép nhân (Ma trận A x B không giống B x A).
  3. Sai dấu khi tính định thức hoặc tìm ma trận nghịch đảo.
  4. Nhầm lẫn giữa hàng (ngang) và cột (dọc) khi nhập dữ liệu.

Ứng dụng thực tế📊

  1. Giải các phương trình tuyến tính trong đại số bằng các phép toán ma trận.

  2. Phân tích các biến đổi dữ liệu trong đồ họa máy tính.

  3. Tối ưu hóa các hệ thống kỹ thuật với các phép tính ma trận.

Câu hỏi và Trả lời

Máy tính ma trận là gì?

Máy tính phép toán ma trận là một loại ứng dụng hỗ trợ thực hiện các phép toán cơ bản hoặc nâng cao như nhân, cộng, trừ, tìm định thức hoặc thậm chí nghịch đảo của các cấu trúc được gọi là ma trận. Các công cụ như vậy rất hữu ích khi xử lý các phép tính phức tạp liên quan đến nhiều bước.

Làm thế nào để thực hiện phép nhân ma trận?

Để thực hiện phép nhân ma trận, số cột của ma trận đầu tiên phải bằng số hàng của ma trận thứ hai. Khi các giá trị được nhập vào máy tính nhân ma trận, sử dụng phương pháp tổng-tích hàng theo cột để tính toán tích của hai ma trận.

Máy tính định thức được sử dụng để làm gì?

Máy tính định thức được sử dụng đặc biệt để tính toán số vô hướng tương ứng với một số mảng vuông nhất định, điều này rất cần thiết trong việc giải các hệ thống với nhiều phương trình tuyến tính hoặc hiểu liệu các ma trận đã cho có thể được nghịch đảo (chuyển vị). Lĩnh vực nghiên cứu này chủ yếu liên quan đến đại số tuyến tính.

Tôi có thể sử dụng bộ giải ma trận cho ma trận 3x3 không?

Có. Máy tính nhân ma trận có thể hoạt động với ma trận 3x3 để tính nghịch đảo, định thức và nhân ma trận. Chỉ cần gửi các giá trị của ma trận và máy tính của bạn sẽ thực hiện tất cả các phép tính với độ chính xác.

Máy tính ma trận trực tuyến tính toán kết quả như thế nào?

Công cụ sử dụng thuật toán dựa trên các phương trình chuẩn: C[i,j] = tổng(A[i,k] * B[k,j]) cho phép nhân. Đối với nghịch đảo, nó sử dụng thuật toán khử Gauss-Jordan để đảm bảo độ chính xác tuyệt đối ngay cả với số thập phân.

Máy tính nghịch đảo ma trận được sử dụng để làm gì?

Ma trận nghịch đảo (ký hiệu là A^-1) là ma trận mà khi nhân với ma trận gốc A sẽ cho ra ma trận đơn vị I. Nó cực kỳ quan trọng trong việc giải phương trình ma trận AX = B bằng cách tính X = A^-1 * B.

Làm thế nào để suy ra ma trận chuyển vị từ một ma trận đã cho?

Ma trận chuyển vị (Transposed Matrix) được tạo ra bằng cách hoán đổi hàng thành cột và cột thành hàng. Nếu phần tử ở hàng i cột j là a(i,j), thì ở ma trận chuyển vị nó sẽ nằm ở hàng j cột i.

Làm thế nào để sử dụng Máy tính Ma trận trong học tập ở Việt Nam?

Sinh viên tại các trường như Đại học Bách Khoa hay Đại học Khoa học Tự nhiên có thể dùng công cụ này để kiểm tra đáp án các bài tập đại số tuyến tính, đặc biệt là các bước khử Gauss hoặc tìm ma trận phụ hợp phức tạp.

🔢Thử Các Máy Tính Khác

Máy Tính Lượng Giác
Máy Tính Logarit
Công Cụ Tính Vòng Tròn
Lưu ý: Máy tính này được thiết kế để cung cấp các ước tính hữu ích cho mục đích thông tin. Mặc dù chúng tôi nỗ lực vì sự chính xác, kết quả có thể thay đổi tùy thuộc vào luật địa phương và hoàn cảnh cá nhân. Chúng tôi khuyên bạn nên tham khảo ý kiến của cố vấn chuyên môn cho các quyết định quan trọng.