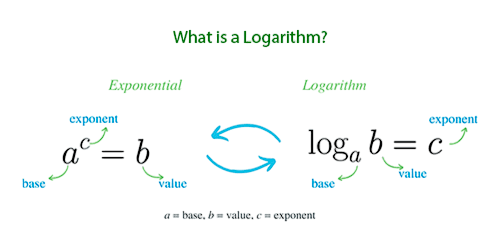Máy Tính Logarit
Thực hiện các tính toán logarit một cách hiệu quả trực tuyến
📋Cách Sử Dụng Máy Tính Log?
-
Nhập giá trị đối số.
-
Chọn hoặc nhập cơ sở logarit.
-
Nhấn tính toán và kết quả của bạn sẽ được hiển thị.
Để sử dụng máy tính log, bạn sẽ nhập trước tiên số mà bạn muốn tìm logarit vào trường đầu tiên. Sau đó, bạn phải nhập cơ sở cho logarit; log phổ biến (cơ sở 10), log tự nhiên (cơ sở e), hoặc bất kỳ cơ sở tùy chỉnh nào, chẳng hạn như log nhị phân mạnh mẽ, ví dụ. Khi tìm log cơ sở 2, bạn chỉ cần nhập 2 làm số cơ sở của bạn và số của bạn. Để tìm log tự nhiên, chọn cơ sở e hoặc sử dụng hàm log tự nhiên. Khi bạn hoàn thành việc nhập các mục nhập của mình, nhấp vào nút tính toán để nhận đầu ra. Công cụ nên hiển thị cho bạn giá trị logarit và bất kỳ thông tin liên quan nào về logarit được tính toán, chẳng hạn như nếu nó là log phổ biến, tự nhiên hoặc cơ sở tùy chỉnh. Hãy chắc chắn rằng các mục nhập của bạn chính xác vì logarit chỉ tồn tại cho số dương hoặc cơ sở bằng hoặc nhỏ hơn 1 hoặc bằng 0, ngoại trừ cơ sở 1. Bạn có thể làm nhiều hơn thế, dù sao; bạn có thể xây dựng trên những gì bạn đã làm, và hoàn thành các tính toán và ứng dụng phức tạp hơn với các kết hợp của các log khác mà bạn đã tính toán.
Mẹo hữu ích💡
-
Xác minh cơ sở lớn hơn 0 và không phải 1 trước khi tính toán.
-
Sử dụng đơn vị nhất quán khi áp dụng log cho dữ liệu thế giới thực.
Cách Các Tính Toán Được Thực Hiện
Máy tính log sử dụng công thức logarit: log_b(a) = ln(a) / ln(b), trong đó ln là logarit tự nhiên. Trong trường hợp cơ sở 10, nó sẽ sử dụng log10(a), và tương tự cho log tự nhiên, ln(a). Các tính toán vượt xa độ chính xác của thư viện toán học tiêu chuẩn vì các tính toán logarit yêu cầu độ chính xác cho nhiều cơ sở (1 hoặc hơn) và cũng cần tránh lỗi bằng cách truyền giá trị không hợp lệ cho các hoạt động logarit. Kết quả logarit được làm tròn đến một số thập phân hợp lý cho sự tự tin của người tiêu dùng. 
Ứng Dụng Thực Tế📊
-
Tính toán sự tăng trưởng dữ liệu cho các thuật toán dựa trên log cơ sở 2.
-
Tính toán sự phân rã mũ cho vật lý dựa trên giá trị log tự nhiên.
-
Chuyển đổi đơn vị dựa trên log cơ sở 10 tiêu chuẩn trong hóa học.
Câu hỏi và Trả lời
Máy tính log là gì?
Máy tính log tính toán một logarit cho một số với cơ sở được chỉ định bởi người dùng. Máy tính log có thể hữu ích khi bạn đang giải quyết các phương trình logarit, hoặc đánh giá một log. Đối với nhu cầu logarit phổ biến, nhiều công cụ miễn phí như CalcMate sẽ cho bạn câu trả lời chính xác.
Cách sử dụng máy tính logarit cho cơ sở 2?
Đối với các chức năng máy tính log cơ sở 2, chỉ cần nhập số của bạn và đặt cơ sở là 2, và nó sẽ tính toán logarit nhị phân của bạn. Điều này thường hữu ích cho tính toán và lý thuyết thông tin.
Máy tính log tự nhiên có thể xử lý giá trị phức tạp không?
Hầu hết các máy tính log tự nhiên chỉ làm việc với số thực dương, vì logarit chỉ được định nghĩa cho số dương trong các trường hợp sử dụng bình thường. Đối với sử dụng nâng cao, bạn có thể muốn tham khảo phần mềm chuyên dụng để đạt được điều này.
Điều gì làm cho máy tính logarit khác biệt so với các máy cơ bản?
Máy tính log có thể chấp nhận bất kỳ cơ sở nào, bao gồm cơ sở do người dùng định nghĩa và đôi khi thậm chí bao gồm công cụ để mở rộng logarit, hoặc đơn giản hóa biểu thức của bạn.
Máy tính log cơ sở 10 trực tuyến chính xác đến mức nào?
Máy tính log cơ sở 10 trực tuyến sử dụng các thuật toán phong phú để cung cấp kết quả với nhiều chữ số thập phân, và do đó cho phép kết quả rất chính xác trong công việc khoa học và kỹ thuật.
Tôi nên sử dụng bộ giải log cho các vấn đề toán học bao nhiêu lần?
Bạn nên sử dụng bộ giải log bất cứ khi nào bạn muốn mô tả một vấn đề với mô hình tăng trưởng/phân rã mũ để bạn có thể kiểm tra tính toán và mẫu của mình.
Các công thức nào được sử dụng trong Máy Tính Log?
Công thức cơ bản của máy tính log là log_b(a) = c, nghĩa là b^c = a. Đối với mục đích tính toán, nó thường sử dụng thay đổi cơ sở: log_b(a) = log_k(a)/log_k(b), cho tất cả k > 0 và k ≠ 1. Thường thì, log tự nhiên (ln) hoặc log phổ biến (log10) được sử dụng để thay đổi cơ sở. Cách tiếp cận thay đổi cơ sở đã được suy ra từ công trình của John Napier, và đã được định nghĩa và phân tích qua nhiều thế kỷ. Các tổ chức, như Liên Minh Toán Học Quốc Tế, đã xác minh các sử dụng công bằng và đúng đắn của việc sử dụng logarit cho các ứng dụng tiêu chuẩn.
Sự khác biệt giữa log và ln là gì?
Log thường đề cập đến log cơ sở 10 (log phổ biến), trong khi ln là log tự nhiên (cơ sở e).
Làm thế nào để tính antilog bằng máy tính này?
Máy tính này tính log, nhưng để tìm antilog, bạn có thể sử dụng lũy thừa: antilog_b(c) = b^c.