Máy Tính Lượng Giác
Tính Hàm Lượng Giác, Góc và Cạnh Tam Giác.
Ví dụ tính toán
Cách Sử Dụng Máy Tính Lượng Giác?
Đầu tiên, bạn hãy chọn đơn vị đo góc là Độ (Degrees) hoặc Radian. Nhập các giá trị đã biết (ví dụ: độ dài một cạnh và một góc, hoặc hai cạnh của tam giác). Sau đó, chọn hàm lượng giác bạn cần tính như Sin, Cos, Tan hoặc các hàm nghịch đảo như Arcsin, Arccos. Nhấn Tính toán để nhận kết quả ngay lập tức. Máy tính cũng hỗ trợ giải toàn bộ các cạnh và góc còn lại của một tam giác vuông một cách tự động.
Cách Thực Hiện Các Phép Tính?
Máy tính lượng giác hoạt động dựa trên các tỷ số cạnh trong tam giác vuông: Sin = Đối / Huyền, Cos = Kề / Huyền, và Tan = Đối / Kề. Đối với các bài toán hình học nâng cao, công cụ sử dụng định lý hàm số Sin và hàm số Cos để giải các tam giác bất kỳ. Tất cả các thuật toán đều tuân thủ tiêu chuẩn toán học của Hiệp hội Toán học quốc tế, đảm bảo độ chính xác đến nhiều chữ số thập phân.
Mẹo hữu ích 💡
- Nhập góc bằng độ hoặc radian theo yêu cầu.
- Xác minh các cạnh hoặc góc đã biết để có kết quả chính xác.
📋Các bước tính toán
-
Chọn chế độ độ hoặc radian.
-
Nhập các góc hoặc độ dài cạnh đã biết.
-
Nhấn "Tính toán" để xem kết quả của các hàm lượng giác.
Những lỗi cần tránh ⚠️
- Xác định sai cạnh đối và cạnh kề so với góc đang xét.
- Để máy tính ở chế độ Radian khi đề bài yêu cầu tính theo Độ (Degree).
- Cố gắng tìm giá trị sin hoặc cos của một góc mà kết quả ra lớn hơn 1.
- Nhầm lẫn hàm ngược (arcsin) với hàm nghịch đảo (cosecant).
Ứng Dụng Thực Tiễn📊
Giải các tam giác vuông cho bài tập hình học.
Xác định góc cho các dự án trong kỹ thuật hoặc vật lý.
Xác định, phân tích và áp dụng các hàm lượng giác vào đồ thị trong giải tích.
Câu hỏi và Trả lời
Lượng giác là gì?
Lượng giác là một nhánh của toán học liên quan đến các góc và cạnh của tam giác, đặc biệt là tam giác vuông. Tên của nó xuất phát từ các từ Hy Lạp có nghĩa là tam giác và đo lường. Lượng giác sử dụng các tỷ số, bao gồm sin (sin), cos (cos) và tan (tan), để giải quyết các vấn đề thực tế trong vật lý, kỹ thuật, thiên văn học và âm nhạc. Lượng giác hữu ích trong việc giải quyết các vấn đề liên quan đến hiện tượng tuần hoàn như sóng hoặc dao động.
Máy tính lượng giác là gì?
Máy tính hàm lượng giác tính toán giá trị của các hàm như sin, cos, tan, cosec, sec và cot dựa trên dữ liệu đầu vào của góc hoặc độ dài cạnh của tam giác. Ngoài ra, nó có thể giúp bạn giải các phương trình lượng giác phức tạp, tính toán các yếu tố dựa trên vòng tròn đơn vị hoặc đơn giản là cho các vấn đề hình học, vật lý hoặc kỹ thuật. CalcMate giúp dễ dàng đánh giá tỷ số của các hàm lượng giác và giải các góc và cạnh chưa biết trong tam giác.
Máy tính lượng giác giải tam giác vuông như thế nào?
Máy tính lượng giác miễn phí của chúng tôi sẽ giải tam giác vuông bằng cách sử dụng hai giá trị đã biết, như một cạnh và một góc, hai cạnh hoặc diện tích và một cạnh. Nhập các giá trị đã xác định vào máy tính, chọn xem bạn muốn một cạnh hay một góc làm kết quả, và máy tính sẽ sử dụng một số hàm, bao gồm tỷ số lượng giác (sin, cos và tan) và các hàm ngược, để xác định giá trị chưa biết của tam giác. Bằng cách này, máy tính sẽ giải các cạnh hoặc góc còn thiếu một cách chính xác và phù hợp với tính tương tự hoặc đồng dạng của tam giác.
Làm thế nào để tính sin, cos, tan cho một tam giác?
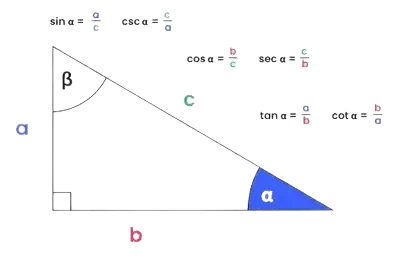
Để tính sin, cos hoặc tan cho một tam giác, nhập độ dài cạnh hoặc góc đã biết vào máy tính lượng giác. Để đo các hàm lượng giác khác nhau, chọn hàm bạn đang tính toán và chỉ định xem bạn đang chọn góc bằng độ hay radian (trừ khi máy tính của bạn chỉ đo ở một chế độ). Khi các tỷ số lượng giác được tính toán, máy tính sẽ tuân theo SOHCAHTOA (sin = cạnh đối/cạnh huyền, cos = cạnh kề/cạnh huyền, tan = cạnh đối/cạnh kề) để tìm các tỷ số lượng giác chính xác mà bạn mong muốn. Điều này hữu ích để giải các bài toán tam giác vuông hoặc thậm chí để kiểm tra các định danh lượng giác.
Tôi có thể sử dụng radian và độ với máy tính không?
Có, máy tính sin, cos và tan hỗ trợ cả radian và độ, điều này giúp dễ dàng xử lý các ngữ cảnh khác nhau trong toán học. Chọn đơn vị ưa thích của bạn trước khi nhập giá trị để đảm bảo rằng nó phù hợp với bài toán đang được giải. Điều này đảm bảo rằng bạn có thể nhận được kết quả chính xác cho các câu hỏi liên quan đến đánh giá vòng tròn đơn vị, vẽ đồ thị các hàm lượng giác hoặc giải các phương trình lượng giác trong các bối cảnh học thuật hoặc chuyên nghiệp.
Máy tính lượng giác trực tuyến chính xác đến mức nào?
Các máy tính lượng giác trực tuyến, như CalcMate, chứa các câu trả lời chính xác cho các biến độ dài được chấp nhận, sử dụng các công thức lượng giác truyền thống được sử dụng trong toán học. Độ chính xác sẽ phụ thuộc vào cách bạn nhập thông tin và chế độ nào bạn đã chọn (độ hoặc radian). Miễn là các dữ liệu đầu vào để tìm các phương trình lượng giác, giá trị cụ thể hoặc phân tích tỷ số được nhập chính xác, máy tính này thường đáng tin cậy.
Những công thức nào được sử dụng trong máy tính lượng giác?
Máy tính với các hàm lượng giác sử dụng các tỷ số lượng giác cơ bản, được biết đến như sin(θ) = cạnh đối/cạnh huyền, cos(θ) = cạnh kề/cạnh huyền và tan(θ) = cạnh đối/cạnh kề và các hàm nghịch đảo cosec(θ) = 1/sin(θ), sec(θ) = 1/cos(θ), cot(θ) = 1/tan(θ). Máy tính cũng sử dụng các hàm ngược (arcsin, arccos, arctan), cho phép giải các góc. Các công thức này được phát triển bởi các nhà toán học như Euclid và được sử dụng bởi các tổ chức như Hiệp hội Toán học Hoa Kỳ, vì vậy bạn có thể tin tưởng để nhận được kết quả có thể tái tạo để giải tam giác và vòng tròn đơn vị.
Lượng giác được sử dụng như thế nào trong xây dựng cầu ở Việt Nam?
Ở Việt Nam, lượng giác rất quan trọng trong xây dựng cầu, như Cầu Rồng ở Đà Nẵng. Các hàm lượng giác giúp tính toán góc và lực để đảm bảo thiết kế cầu an toàn và ổn định, đặc biệt trong điều kiện địa hình phức tạp như sông ngòi và vùng núi.
Lưu ý: Máy tính này được thiết kế để cung cấp các ước tính hữu ích cho mục đích thông tin. Mặc dù chúng tôi nỗ lực vì sự chính xác, kết quả có thể thay đổi tùy thuộc vào luật địa phương và hoàn cảnh cá nhân. Chúng tôi khuyên bạn nên tham khảo ý kiến của cố vấn chuyên môn cho các quyết định quan trọng.