Trigonometrie Rechner

Lösen Sie komplexe Dreiecksaufgaben mit präzisen Winkelfunktionen.

Berechnungsbeispiele

Berechnungsfall Ergebnis
Tangens von 45° 1
Arkussinus von 0,5 (asin 0.5) 30°
Berechnung der Ankathete bei Hypotenuse 10 und 60° 5

Wie verwende ich den Trigonometrie-Rechner?

Wählen Sie zunächst, ob Sie mit Gradmaß (DEG) oder Bogenmaß (RAD) rechnen möchten. Geben Sie dann die bekannten Seitenlängen (Ankathete, Gegenkathete, Hypotenuse) oder einen Winkel ein. Unser Rechner nutzt die SOH-CAH-TOA Logik, um alle fehlenden Werte im Handumdrehen zu ermitteln. Dies ist besonders hilfreich für Schüler in der Sekundarstufe II zur Vorbereitung auf das Abitur oder für Handwerker zur Berechnung von Dachschrägen und Winkelschnitten.

Wie Werden die Berechnungen Durchgeführt?

Der Trigonometrie-Rechner verwendet standardmäßige trigonometrische Verhältnisse: Sinus(θ) = Gegenkathete/Hypotenuse, Kosinus(θ) = Ankathete/Hypotenuse und Tangens(θ) = Gegenkathete/Ankathete. Für die reziproken Funktionen gilt Kosekans(θ) = 1/Sinus(θ), Sekans(θ) = 1/Kosinus(θ) und Kotangens(θ) = 1/Tangens(θ). Um Winkel zu berechnen, werden inverse Funktionen wie Arcsinus, Arccosinus oder Arctangens verwendet. Die Berechnungen des Rechners basieren auf unterschiedlichen Eingabewerten, und die Lösungen erfolgen durch etablierte Funktionen, die in der mathematischen Gemeinschaft akzeptiert sind, zur Überprüfung durch Quellen wie die American Mathematical Association.

Diagramm der Trigonometrischen Funktionen

Nützliche Tipps 💡

  • Gib Winkel in Grad oder Radiant ein, wie erforderlich.
  • Überprüfe bekannte Seiten oder Winkel für präzise Ergebnisse.

📋Schritte zur Berechnung

  1. Wählen Sie den Modus Grad oder Radiant.

  2. Geben Sie bekannte Winkel oder Seitenlängen ein.

  3. Drücken Sie "Berechnen", um die Ergebnisse der trigonometrischen Funktionen anzuzeigen.

Häufige Fehler ⚠️

  1. Grad verwenden wenn der Taschenrechner auf Bogenmaß steht oder umgekehrt.
  2. Vergessen dass Arcusfunktionen nur Hauptwerte liefern.
  3. Denken sin⁻¹(sin x) = x für jeden x gilt nur im Bereich -π/2 bis π/2.
  4. Ankathete/Hypotenuse mit Gegenkathete/Hypotenuse verwechseln.

Praktische Anwendungen📊

  1. Lösen von rechtwinkligen Dreiecken für Geometrieaufgaben.

  2. Bestimmen von Winkeln für Projekte in Ingenieurwesen oder Physik.

  3. Erkennung, Analyse und Anwendung trigonometrischer Funktionen in Graphen der Analysis.

Fragen und Antworten

Was ist Trigonometrie?

Die Trigonometrie ist ein Teilgebiet der Mathematik, das sich mit den Winkeln und Seiten von Dreiecken, insbesondere rechtwinkligen Dreiecken, beschäftigt. Der Name stammt von den griechischen Wörtern für Dreieck und Messung. Die Trigonometrie verwendet Verhältnisse, einschließlich Sinus (sin), Kosinus (cos) und Tangens (tan), um reale Probleme in Physik, Ingenieurwesen, Astronomie und Musik zu lösen. Die Trigonometrie ist nützlich zur Lösung von Problemen, die periodische Phänomene wie Wellen oder Schwingungen betreffen.

Was ist ein Trigonometrie-Rechner?

Ein Trigonometrie-Rechner berechnet Funktionen wie Sinus, Kosinus, Tangens oder deren Inverse basierend auf Winkel oder Seitenlängen. Mit CalcMate lösen Sie Dreiecke oder Gleichungen für Geometrie, Physik oder Ingenieurwesen präzise.

Wie löst ein Trigonometrie-Rechner rechtwinklige Dreiecke?

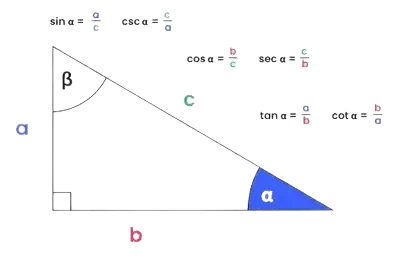
Geben Sie zwei bekannte Werte (z. B. Seite und Winkel) ein. Der Rechner verwendet SOHCAHTOA (Sinus = Gegenkathete/Hypotenuse, Kosinus = Ankathete/Hypotenuse, Tangens = Gegenkathete/Ankathete), um fehlende Seiten oder Winkel zu berechnen.

Was ist der Unterschied zwischen Grad und Radiant?

Das Gradmaß (0-360°) ist im Alltag üblich, während das Bogenmaß (Radiant) in der höheren Mathematik und Analysis verwendet wird (π entspricht 180°).

Was bedeutet SOH-CAH-TOA?

Es ist eine Eselsbrücke für die Verhältnisse: Sinus = Opposite/Hypotenuse, Cosinus = Adjacent/Hypotenuse, Tangens = Opposite/Adjacent. Im Deutschen nutzen wir oft G-A-G-A (Gegenkathete, Ankathete).

Kann der Rechner auch nicht-rechtwinklige Dreiecke lösen?

Für allgemeine Dreiecke sollten Sie zusätzlich den Sinussatz oder Kosinussatz anwenden, wobei dieser Rechner die Basis-Winkelfunktionen liefert.

Welche Formeln werden im Trigonometri Rechner verwendet?

Formeln: sin(θ) = Gegenkathete/Hypotenuse, cos(θ) = Ankathete/Hypotenuse, tan(θ) = Gegenkathete/Ankathete; Inverse: arcsin, arccos, arctan. Diese entsprechen Standards von Euklid und der MAA.

🔢Weitere Rechner Ausprobieren

Logarithmus Rechner
Kreisrechner
Volumen Rechner
Hinweis: Dieser Rechner dient dazu, hilfreiche Schätzungen zu Informationszwecken bereitzustellen. Obwohl wir uns um Genauigkeit bemühen, können die Ergebnisse je nach örtlichen Gesetzen und individuellen Umständen variieren. Wir empfehlen, bei wichtigen Entscheidungen einen professionellen Berater zu Rate zu ziehen.