Trigonometri Hesaplama Aracı

Üçgenlerin gizemini çözün. Açı ve kenar değerlerini kullanarak tüm trigonometrik fonksiyonlara anında ulaşın.

Hesaplama Örnekleri

Hesaplama Durumu Sonuç
arctan(1) değerini bul 45°
Radyanı dereceye çevir (π/2 rad) 90°
Kosünüs teoremi ile kenar bulma a² = b² + c² - 2bc.cos(A)

Trigonometri Hesaplayıcı Nasıl Kullanılır?

Hesaplamaya başlamadan önce derece veya radyan modunu seçin. Bilinen değerleri (örneğin bir açı ve bir kenar uzunluğu) ilgili alanlara girin. Aracımız; sinüs, kosinüs, tanjant, kosekant, sekant ve kotanjant değerlerini saniyeler içinde sunar. Dik üçgen problemleri veya birim çember üzerindeki karmaşık sorular için en güvenilir yardımcınızdır.

Matematiksel Formüller ve Temel Oranlar

Trigonometri hesaplayıcımız temel geometrik oranları kullanır: Sinüs (sinθ) = Karşı / Hipotenüs, Kosinüs (cosθ) = Komşu / Hipotenüs ve Tanjant (tanθ) = Karşı / Komşu. Ters fonksiyonlar (arcsin, arccos, arctan) ile bilinen kenarlardan bilinmeyen açıları bulmanızı sağlar. Bu hesaplamalar, Öklid geometrisi ve modern matematik topluluğu tarafından kabul edilen yerleşik algoritmalarla gerçekleştirilir.Trigonometrik Fonksiyon Diyagramı

Uzman Tavsiyeleri 💡

  • Açının hangi bölgede (1, 2, 3 veya 4) olduğunu kontrol ederek işaretleri (artı/eksi) teyit edin.
  • Hassas mühendislik hesaplamaları için en az iki kenar veya bir kenar-bir açı bilgisini doğru girdiğinizden emin olun.

📋Hesaplama Adımları

  1. Hesaplama birimini (Derece veya Radyan) belirleyin.

  2. Üçgene ait bilinen açı veya kenar uzunluklarını kutucuklara yazın.

  3. Tüm sonuçları ve çözüm dökümünü görmek için "Hesapla"ya basın.

Kaçınılması Gereken Hatalar ⚠️

  1. Açının konumuna göre karşı ve komşu kenarları karıştırmak.
  2. Derece yerine Radyan modunda (veya tersi) işlem yapmak.
  3. Sinüs veya kosinüs değerlerinin mutlak değerce 1'den büyük olabileceğini düşünmek.
  4. Ters trigonometrik fonksiyonlar ile çarpmaya göre ters fonksiyonları karıştırmak.

Pratik Uygulamalar📊

  1. Geometri derslerinde dik üçgenleri çözmek.

  2. Mühendislik veya fizik projelerinde açıları belirlemek.

  3. Kalkülüs grafiklerinde trigonometrik fonksiyonları tanımlamak, analiz etmek ve uygulamak.

Sıkça Sorulan Sorular (SSS)

Trigonometri nedir?

Trigonometri, üçgenlerin açıları ve kenarlarıyla, özellikle dik üçgenlerle ilgilenen bir matematik dalıdır. Adı, Yunanca üçgen ve ölçü anlamına gelen kelimelerden türemiştir. Trigonometri, sinüs (sin), kosinüs (cos) ve tanjant (tan) gibi oranları kullanarak fizik, mühendislik, astronomi ve müzikte gerçek dünya problemlerini çözmek için kullanılır. Trigonometri, dalgalar veya salınımlar gibi periyodik fenomenleri çözmek için kullanışlıdır.

Trigonometri hesaplayıcı nedir?

Trigonometrik fonksiyon hesaplayıcı, bir üçgenin açısı veya kenar uzunluğu girişine dayanarak sinüs, kosinüs, tanjant, kosekant, sekant ve kotanjant gibi trigonometrik fonksiyonların değerini hesaplar. Ayrıca, karmaşık trigonometrik denklemleri çözmeye, birim çemberine dayalı öğeleri hesaplamaya veya geometri, fizik veya mühendislik problemleri için kullanılabilir. CalcMate, trigonometrik fonksiyonların oranlarını değerlendirmeyi ve üçgenlerde bilinmeyen açıları ve kenarları çözmeyi kolaylaştırır.

Dik üçgenler için geometri hesaplama aracı nasıl çalışır?

İki bilinen değeri (kenar, açı) girin, trigonometrik oranlar (SOHCAHTOA) ve ters fonksiyonlarla eksik değerleri çözer.

Sinüs, kosinüs, tanjant nasıl hesaplanır?

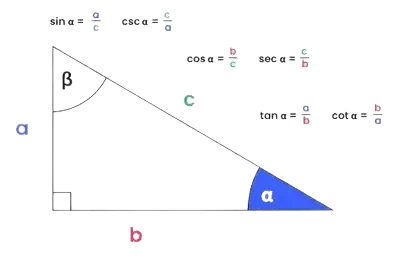
Kenar veya açıyı geometri hesaplama aracına girin, SOHCAHTOA (sin = karşı/hipotenüs, cos = bitişik/hipotenüs, tan = karşı/bitişik) ile hesaplar.

Geometri hesaplama aracında radyan ve derece kullanılabilir mi?

Evet, radyan veya derece seçerek birim çemberi veya denklemleri doğru bir şekilde çözer.

Çevrimiçi geometri hesaplama aracı ne kadar doğrudur?

Doğru girişlerle (derece/radyan) matematiksel formüllere dayalı güvenilir sonuçlar sunar, Öklid standartlarıyla uyumludur.

Geometri hesaplama aracında hangi formüller kullanılır?

Sinüs(θ) = karşı/hipotenüs, kosinüs(θ) = bitişik/hipotenüs, tanjant(θ) = karşı/bitişik ve ters fonksiyonlar, MAA tarafından onaylanmıştır.

🔢Daha Fazla Hesap Makinesi Deneyin

Logaritma Hesaplayıcısı
Çember Hesaplayıcı
Hacim Hesaplayıcı
Not: Bu hesaplayıcı, bilgilendirme amaçlı faydalı tahminler sunmak için tasarlanmıştır. Doğruluk için çaba göstersek de sonuçlar yerel yasalara ve bireysel durumlara göre değişiklik gösterebilir. Önemli kararlar için profesyonel bir danışmana başvurmanızı öneririz.