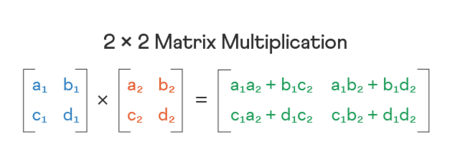Calculateur de Matrices

Simplifiez Vos Opérations sur Matrices pour les Études ou l’Ingénierie.

Veuillez entrer les détails requis et cliquer sur Calculer.

Exemples de calcul

Cas de calcul Résultat
Déterminant d'une matrice 2x2 [[5,2],[3,4]] 14
Produit matriciel de A (3x2) par B (2x3) Résultat : Matrice 3x3
Inversion d'une matrice carrée pour résoudre un système Matrice A⁻¹

Comment utiliser le calculateur de matrices ?

Sélectionnez l’opération souhaitée (addition, soustraction ou multiplication). Entrez les dimensions de vos matrices. Pour la multiplication, vérifiez que le nombre de colonnes de la matrice A égale le nombre de lignes de la matrice B. Remplissez les éléments et cliquez sur Calculer pour obtenir le résultat étape par étape.

Comment les calculs de matrices sont-ils effectués ?

L’addition et la soustraction se font élément par élément sur des matrices de même taille. La multiplication utilise la règle de la ligne par la colonne. Pour les déterminants, nous appliquons la règle de Sarrus pour les matrices 3x3 et la réduction de ligne pour les plus grandes. En France, ces méthodes sont au cœur du programme de classes préparatoires et d’ingénierie, permettant de résoudre des systèmes d’équations complexes ou des transformations 3D.Diagramme de la Multiplication de Matrices

Conseils d’Experts 💡

  • Vérifiez la compatibilité des dimensions avant de multiplier.
  • Une matrice doit être carrée pour posséder un déterminant ou une inverse.

📋Étapes de calcul

  1. Choisissez l’opération (addition, multiplication, déterminant, inverse).

  2. Configurez la taille de vos matrices.

  3. Saisissez les nombres et cliquez sur "Calculer".

Erreurs à éviter ⚠️

  1. Tenter de multiplier des matrices dont les dimensions ne sont pas compatibles.
  2. Ne pas respecter l'ordre de multiplication (A x B n'est pas égal à B x A).
  3. Faire des erreurs de signe lors du calcul du déterminant ou de l'inverse.
  4. Confondre les lignes (horizontales) avec les colonnes (verticales) lors de la saisie.

Applications pratiques📊

  1. Résoudre des équations linéaires en algèbre à l’aide d’opérations sur les matrices.

  2. Analyser les transformations de données dans les graphiques informatiques.

  3. Optimiser les systèmes d’ingénierie avec des calculs de matrices.

Questions Fréquentes (FAQ)

Qu’est-ce qu’un calculateur de matrices ?

Un calculateur d’opérations sur les matrices est un type d’application qui prend en charge l’exécution d’opérations de base ou avancées comme la multiplication, l’addition, la soustraction, la recherche de déterminants ou même d’inverses de structures appelées matrices. Ces outils sont très utiles pour gérer des calculs complexes impliquant plusieurs étapes.

Comment effectuer une multiplication de matrices ?

Pour effectuer une multiplication de matrices, les colonnes de la première matrice doivent être égales aux lignes de la seconde matrice. Une fois les valeurs entrées dans le calculateur de multiplication de matrices, utilisez la méthode de somme-produit ligne par colonne pour calculer le produit des deux matrices.

À quoi sert un calculateur de déterminant ?

Les calculateurs de déterminants sont utilisés spécifiquement pour calculer la quantité scalaire correspondant à certains tableaux carrés, ce qui est essentiel pour résoudre des systèmes avec plusieurs équations linéaires ou pour comprendre si des matrices données peuvent être inversées (transposées). Ce domaine d’étude concerne principalement l’algèbre linéaire.

Puis-je utiliser un solveur de matrices pour des matrices 3x3 ?

Oui. Un calculateur de multiplication de matrices peut travailler avec des matrices 3x3 pour obtenir des inverses, calculer des déterminants et multiplier des matrices. Soumettez simplement les valeurs de la matrice et votre calculateur effectuera tous les calculs avec précision.

Comment le calculateur de matrices en ligne calcule-t-il les résultats ?

Le calculateur de matrices effectue tous les calculs basés sur des équations d’algèbre linéaire standard. Par exemple, C[i,j] = Σ(A[i,k] * B[k,j]) est la manière dont la multiplication de matrices est calculée avec les matrices d’entrée : A et B. Les déterminants sont calculés en utilisant ad - bc pour les matrices 2x2, et vous pouvez développer le long d’une ligne ou d’une colonne pour les matrices 3x3. Les inverses utilisent l’élimination de Gauss. Ces équations ont été vérifiées selon des normes mathématiques, donc les résultats seront précis.

À quoi sert un calculateur de matrice inverse ?

Un calculateur de matrice inverse calcule l’inverse d’une matrice carrée, notée $A^{-1}$, où $A \times A^{-1} = I$ (matrice identité). Il est crucial pour résoudre des systèmes d’équations linéaires, transformer des coordonnées et analyser des transformations linéaires dans des domaines comme la physique et l’ingénierie. Entrez les valeurs de la matrice, assurez-vous qu’elle est carrée et inversible (déterminant non nul), et l’outil calcule l’inverse à l’aide de méthodes comme l’élimination de Gauss.

Comment dériver des matrices transposées à partir d’une matrice donnée ?

Pour trouver la transposée d’une matrice, vous pouvez utiliser un calculateur de matrice transposée pour interchanger les lignes et les colonnes de la matrice, reflétant la matrice sur sa diagonale, transformant les colonnes en lignes et vice versa. Pour une matrice $ A $ avec des entrées individuelles $ a_{i,j} $, la transposée $ A^T $ a les entrées $ a_{j,i} $. Après avoir entré la taille et les valeurs de la matrice, la matrice transposée obtenue est affichée instantanément. Cela complète et soutient l’analyse de données, l’apprentissage automatique et les applications d’algèbre linéaire.

🔢Outils Recommandés

Calculateur de Trigonométrie
Calculateur de Logarithmes
Calculateur Cercle
Note : Ce calculateur est conçu pour fournir des estimations utiles à des fins d'information. Bien que nous fassions tout notre possible pour garantir l'exactitude, les résultats peuvent varier en fonction des lois locales et des circonstances individuelles. Nous vous recommandons de consulter un conseiller professionnel pour toute décision importante.