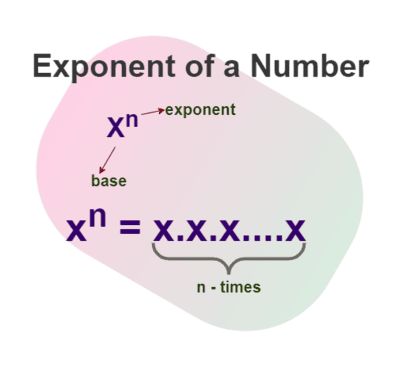Calculatrice d'Exposants

Déterminez les puissances et exposants en utilisant cet outil pour des opérations d'exponentiation.

Résultat

Ce calculateur vous a-t-il été utile ?

★ ★ ★ ★ ★
4.9/5 (16 votes)

Exemples de calcul

Cas de calcul Résultat
Calcul de 2 à la puissance 8 (2⁸) 256
Exposant négatif : 10⁻³ 0,001
Puissance d'un nombre décimal (1,1²) 1,21

Comment Utiliser la Calculatrice d'Exposants ?

Commencez à utiliser la calculatrice d'exposants en entrant une base ou un nombre original dans la première boîte ; cela servira de nombre base dans l'exponentiation. Entrez maintenant une valeur d'exposant indiquant le nombre de fois que la base doit se multiplier par elle-même, qu'il s'agisse d'entiers positifs, de nombres négatifs ou même d'exposants fractionnaires si la partie fractionnaire n'est pas une approximation, car elle sera calculée à cette étape. Si vous travaillez avec une notation scientifique ou des points décimaux, assurez-vous de sélectionner l'unité de mesure ou le formatage correct. Une fois terminé, appuyez sur le bouton calculer et il calculera votre entrée et renverra votre sortie.

La réponse fournie reflétera généralement la valeur calculée avec d'autres détails liés à votre entrée, comme l'expression originale renvoyée sous les informations de la base calculée. Par exemple, si la base d'un nombre est 2 et que vous définissez l'exposant à 5, il vous donnera la réponse calculée de 32, (qui est la multiplication basique de la base du nombre).

Comment les Exposants Sont Calculés

Un nombre base élevé à un exposant signifie multiplication répétée du nombre base par lui-même autant de fois que l'indique l'exposant. Pour les exposants entiers positifs : 3^4 indique que 3 est multiplié 4 fois, ou 3×3×3×3=81. Les exposants entiers négatifs indiquent l'inverse : 2^-3=1/(2^3)=1/8. Les exposants fractionnaires indiquent des racines et représentent aussi des puissances : 16^(1/2)=4 représente la "racine carrée de 16". La calculatrice utilise de grandes valeurs avec des estimations de logarithmes pour maximiser l'efficacité tout en produisant des résultats précis à des décimales standard. Les principes décrits sont des standards acceptés en mathématiques, affirmés par des autorités mathématiques et, en tant que tels, les résultats seront cohérents dans les pratiques de calcul de puissances et d'exponentiation.Qu'est-ce que l'Exposant d'un Nombre ?

Conseils d’Experts 💡

  • Vérifiez les grands exposants avec des contrôles logarithmiques pour éviter les débordements.
  • Convertissez les fractions en décimales pour des entrées de puissances fractionnaires plus fluides.

📋Étapes de calcul

  1. Entrez le nombre base clairement.

  2. Entrez la valeur de l'exposant ensuite.

  3. Appuyez sur calculer pour le résultat.

Erreurs à éviter ⚠️

  1. Multiplier la base par l'exposant (ex: croire que 2 puissance 3 fait 6 au lieu de 8).
  2. Mal appliquer la règle des exposants négatifs (qui donnent des fractions).
  3. Penser que n'importe quel nombre élevé à la puissance zéro donne zéro (le résultat est 1).
  4. Confondre l'addition de puissances avec la multiplication de puissances de même base.

Applications Pratiques📊

  1. Simplifiez les expressions algébriques dans les devoirs ou examens.

  2. Modélisez les taux de croissance en finance en utilisant des fonctions exponentielles.

  3. Vérifiez les données scientifiques impliquant des puissances de dix.

Questions Fréquentes (FAQ)

Qu'est-ce qu'une calculatrice d'exposants ?

Une calculatrice d'exposants détermine efficacement le résultat d'élever un nombre à un exposant ou puissance spécifique représentée par un autre nombre non base. Elle fonctionne avec des nombres entiers, négatifs et fractions pour résoudre rapidement les problèmes mathématiques, facilitant le calcul de puissances et l'exponentiation.

Comment fonctionne une calculatrice de puissances pour les exposants négatifs ?

Une calculatrice de puissances traite un exposant négatif en prenant le réciproque de la base élevée à cet exposant écrit de manière positive. Ainsi, elle traite 5^-2 comme 1/25. Cela est utile pour les problèmes de division liés à l'exponentiation.

Pour quoi puis-je utiliser une calculatrice d'exposants en mathématiques quotidiennes ?

Une calculatrice d'exposants est une façon pratique d'évaluer des expressions mathématiques comme 2^10 ou 3^4 dans le cadre de la simplification d'une équation en milieu académique, ou dans des parties de mathématiques de base, incluant des opérations de puissances.

Pourquoi choisir une calculatrice exponentielle pour les puissances fractionnaires ?

Une calculatrice d'exposants évalue les exposants fractionnaires en combinant racines et multiplications, par exemple 8^(2/3)=4, ce qui aide dans des calculs qui semblent compliqués lors de l'évaluation de la racine dans des contextes d'exponentiation.

Comment calculer 2 à la puissance de 5 avec précision ?

Pour calculer deux élevé à la puissance de cinq, multipliez deux par lui-même cinq fois ; c'est-à-dire 2×2×2×2×2=32, qui est une multiplication répétée simple établie dans les règles d'arithmétique de base pour les puissances.

Une calculatrice avec exposants peut-elle gérer les lois des exposants ?

Oui, même une calculatrice d'exposants utilise des règles comme multiplier des bases identiques en additionnant les exposants : (x^2)(x^3)=x^5, ce qui en fait des moyens pratiques pour les calculs algébriques en exponentiation.

Quelles formules sont utilisées dans la Calculatrice d'Exposants ?

La calculatrice d'exposants utilise l'équation de base d'exponentiation, a^b = a × a × a ×… (b fois) pour les entiers positifs, puis pour les entiers négatifs, elle est définie a^(-b) = 1/(a^b), et pour les fractions, a^(p/q) = (a^p)^(1/q). Chaque définition dérive d'opérations de base et de fonctions où l'exponentiation est utilisée depuis des centaines d'années en algèbre, influencée par des éducateurs comme le National Council of Teachers of Mathematics (NCTM).

🔢Outils Recommandés

Calculateur Binaire
Calculateur de Racine
Calculateur de Formule Quadratique
Note : Ce calculateur est conçu pour fournir des estimations utiles à des fins d'information. Bien que nous fassions tout notre possible pour garantir l'exactitude, les résultats peuvent varier en fonction des lois locales et des circonstances individuelles. Nous vous recommandons de consulter un conseiller professionnel pour toute décision importante.