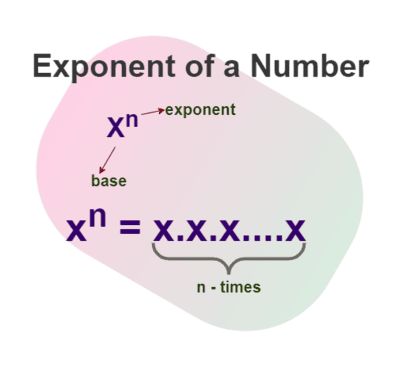Exponenten Rechner
Berechnen Sie mathematische Potenzen mit beliebigen Basen und Exponenten.
📋Wie benutze ich den Exponenten-Rechner?
-
Geben Sie die Basiszahl klar ein.
-
Geben Sie den Exponentenwert als Nächstes ein.
-
Drücken Sie Berechnen für das Ergebnis.
Geben Sie zuerst die Basis (die Zahl, die multipliziert wird) in das erste Feld ein. Tragen Sie dann den Exponenten (die Hochzahl) ein. Unser Rechner unterstützt nicht nur positive Ganzzahlen, sondern auch negative Exponenten und Brüche.
Sobald Sie auf „Berechnen“ klicken, führt das Tool die Exponentiation aus. Wenn Sie zum Beispiel 2 als Basis und 5 als Exponenten wählen, multipliziert der Rechner 2 × 2 × 2 × 2 × 2 und gibt das Ergebnis 32 aus. Für wissenschaftliche Berechnungen oder komplexe Hausaufgaben ist dieser Rechner eine enorme Zeitersparnis, da er auch sehr große Zahlen und Dezimalpotenzen fehlerfrei verarbeitet.
Nützliche Tipps💡
-
Überprüfen Sie große Exponenten mit logarithmischen Checks auf Überlauf.
-
Wandeln Sie Brüche in Dezimalzahlen um für glattere Eingaben fraktioneller Potenzen.
Häufige Fehler ⚠️
- a^(-b) als -(a^b) rechnen statt korrekt 1/a^b.
- Reihenfolge der Potenzen vergessen 2^3^2 sind 2^(3^2) = 512 und nicht (2^3)^2 = 64.
- Prozentzahl direkt als Exponent verwenden 5 % als 5 statt als 0.05.
- e^x mit ln(x) durcheinanderbringen.
Wie Exponenten Berechnet Werden
Eine Basiszahl hoch einem Exponenten bedeutet wiederholte Multiplikation der Basiszahl mit sich selbst so oft, wie vom Exponenten angegeben. Für positive ganzzahlige Exponenten: 3^4 bedeutet, dass 3 viermal multipliziert wird, oder 3×3×3×3=81. Negative ganzzahlige Exponenten bedeuten das Inverse: 2^-3=1/(2^3)=1/8. Fraktionelle Exponenten bedeuten Wurzeln und stellen auch Potenzen dar: 16^(1/2)=4 stellt die "Quadratwurzel von 16" dar.
Der Rechner verwendet große Werte mit Logarithmus-Schätzungen, um Effizienz zu maximieren, während er genaue Ergebnisse bis zu Standarddezimalstellen liefert. Die beschriebenen Prinzipien sind akzeptierte Standards in der Mathematik, bestätigt von mathematischen Autoritäten, und somit sind die Ergebnisse konsistent in den Praktiken der Potenzberechnung und Exponentiation.
Praktische Anwendungen📊
-
Schule & Studium: Lösen von algebraischen Gleichungen und Hausaufgaben.
-
Finanzen: Berechnung von Zinseszinseffekten über lange Zeiträume.
-
Wissenschaft: Arbeit mit der wissenschaftlichen Schreibweise (Zehnerpotenzen).
Fragen und Antworten
Was ist ein Exponenten-Rechner?
Ein Exponenten-Rechner bestimmt effizient das Ergebnis, ein Zahl zu einem spezifischen Exponenten oder Potenz hochzurechnen, dargestellt durch eine andere Nicht-Basiszahl. Er arbeitet mit ganzen Zahlen, negativen Zahlen und Brüchen, um mathematische Probleme schnell zu lösen, und erleichtert die Potenzberechnung und Exponentiation.
Wie funktioniert ein Potenz-Rechner für negative Exponenten?
Ein Potenz-Rechner behandelt einen negativen Exponenten, indem er den Kehrwert der Basis zu diesem Exponenten nimmt, geschrieben positiv. Also behandelt er 5^-2 wie 1/25. Das ist hilfreich bei Divisionsproblemen.
Wofür kann ich einen Exponenten-Rechner im täglichen Mathe verwenden?
Ein Exponenten-Rechner ist eine bequeme Möglichkeit, mathematische Ausdrücke wie 2^10 oder 3^4 zu bewerten, als Teil der Vereinfachung einer Gleichung in einem akademischen Umfeld oder in grundlegender Mathematik, einschließlich Potenzoperationen.
Was bedeutet eine negative Hochzahl?
Ein negativer Exponent führt dazu, dass die Zahl „unter den Bruchstrich“ wandert. a⁻ⁿ ist gleich 1/aⁿ.
Was passiert bei einem Exponenten von 0?
Jede Zahl (außer Null) hoch Null ergibt mathematisch immer 1.
Kann ich Wurzeln mit diesem Rechner ziehen?
Ja, indem Sie Brüche als Exponenten verwenden. Hoch 0,5 entspricht beispielsweise der Quadratwurzel.
Welche Formeln werden im Exponenten-Rechner verwendet?
Der Exponenten-Rechner verwendet die grundlegende Exponentiationsgleichung, a^b = a × a × a ×… (b Mal) für positive Ganzzahlen, dann für negative Ganzzahlen a^(-b) = 1/(a^b), und für Brüche a^(p/q) = (a^p)^(1/q). Jede Definition leitet sich von grundlegenden Operationen und Funktionen ab, wo Exponentiation seit Hunderten von Jahren in der Algebra verwendet wird, beeinflusst von Pädagogen wie dem National Council of Teachers of Mathematics (NCTM).