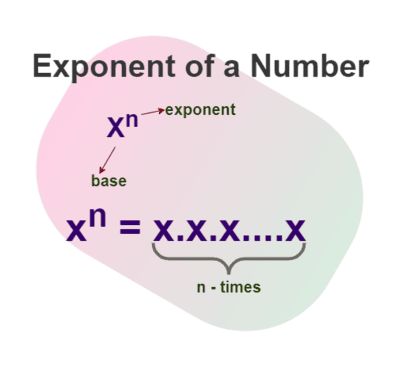Üs Hesaplayıcısı
Bu çevrimiçi araçla güçleri ve üsleri belirleyin, hassas üsleme işlemleri için.
📋Üs Hesaplayıcısını Nasıl Kullanılır?
-
Temel sayıyı net girin.
-
Üs değerini sonra girin.
-
Hesapla'ya basın sonuç için.
Üs hesaplayıcısını kullanmaya, bir temel veya orijinal sayı girerek başlayın ilk kutuya; bu üslemede temel sayı olarak hizmet verecek. Şimdi temel sayının kendisiyle kaç kez çarpılması gerektiğini belirten bir üs değeri girin, pozitif tam sayılar, negatif sayılar veya hatta fraksiyonel üsler olsun eğer fraksiyonel kısım bir yaklaşık değilse bu aşamada hesaplanacak. Bilimsel notasyon veya ondalık noktalarla çalışıyorsanız, doğru ölçü birimini veya formatı seçtiğinizden emin olun. Bitirdiğinizde hesapla düğmesine basın ve girişinizi hesaplayıp çıktınızı döndürür.
Verilen cevap genellikle hesaplanan değeri yansıtır birlikte girişinizle ilgili diğer detaylarla orijinal ifadeyi hesaplanan temel bilgisi altında size geri verir. Örneğin, bir sayının temeli 2 ise ve üssü 5 olarak belirtirseniz, size 32 hesaplanmış cevabı verir, (ki bu sayının temelinin temel katıdır).
Faydalı İpuçları💡
-
Taşma için büyük üsleri logaritmik kontrollerle doğrulayın.
-
Fraksiyonel güç girdileri için kesirleri ondalıklara dönüştürün.
Üsler Nasıl Hesaplanır
Bir temel sayı bir üsse yükseltilmesi temel sayının kendisiyle tekrarlı çarpımını üs tarafından belirtilen kadar kez anlamına gelir. Pozitif tam sayı üsleri için: 3^4 3'ün 4 kez çarpıldığını gösterir, veya 3×3×3×3=81. Negatif tam sayı üsleri tersi anlamına gelir: 2^-3=1/(2^3)=1/8. Fraksiyonel üsler kökleri ve güçleri de temsil eder: 16^(1/2)=4 "16'nın karekökü"nü temsil eder. Hesaplayıcı verimliliği maksimize etmek için logaritma tahminleri ile büyük değerler kullanır standart ondalık basamaklara doğru sonuçlar üretirken. Tanımlanan ilkeler matematikte kabul edilen standartlardır, matematiksel otoriteler tarafından onaylanmış ve bu nedenle sonuçlar güç hesaplama ve üsleme uygulamalarında tutarlı olacaktır.
Pratik Uygulamalar📊
-
Ödev veya sınavlarda cebirsel ifadeleri basitleştirin.
-
Finansta üstel fonksiyonlar kullanarak büyüme oranlarını modelleyin.
-
Onun güçlerini içeren bilimsel verileri doğrulayın.
Soru ve Cevaplar
Üs hesaplayıcısı nedir?
Bir üs hesaplayıcısı bir sayıyı belirli bir üsse veya güce kaldırmanın sonucunu verimli bir şekilde belirler başka bir temel olmayan sayı tarafından temsil edilen. Tam sayılar, negatif sayılar ve kesirlerle çalışır matematik problemlerini hızlı çözmek için, güç hesaplama ve üslemeyi kolaylaştırır.
Güç hesaplayıcısı negatif üsler için nasıl çalışır?
Bir güç hesaplayıcısı negatif üssü temel pozitif yazılmış üsse kaldırmanın karşılıklısını alarak hâlâ işler. Yani 5^-2'yi 1/25 olarak işler. Bu bölme tipi problem için yardımcıdır.
Günlük matematikte üs hesaplayıcısını ne için kullanabilirim?
Üs hesaplayıcısı akademik ortamda bir denklemi basitleştirmenin parçası olarak 2^10 veya 3^4 gibi matematiksel ifadeleri değerlendirmenin pratik bir yoludur, veya temel matematik parçalarında, güç işlemleri dahil.
Neden fraksiyonel güçler için üstel hesaplayıcı seçilir?
Bir üs hesaplayıcısı kökleri ve çarpımları birleştirerek fraksiyonel üsleri değerlendirir, örneğin 8^(2/3)=4, kök değerlendirildiğinde karmaşık görünen hesaplamalarda yardımcı olur.
2'nin 5'inci gücünü nasıl doğru hesaplanır?
Beşinci güce iki kaldırmak için ikiyi kendisiyle beş kez çarpın; yani, 2×2×2×2×2=32, ki bu temel aritmetik kurallarına göre basit tekrarlı çarpımdır.
Üslerle hesaplayıcı üs yasalarını işleyebilir mi?
Evet, hatta üs yapan bir hesaplayıcı aynı temellerin çarpımının üsleri toplamak gibi kurallar kullanır: (x^2)(x^3)=x^5, yani cebirsel hesaplamalar için pratik yollardır.
Üs Hesaplayıcısı'nda hangi formüller kullanılır?
Üs hesaplayıcısı temel üsleme denklemini kullanır, a^b = a × a × a ×… (b kez), pozitif tam sayılar için, sonra negatif tam sayılar için a^(-b) = 1/(a^b) tanımlanır, ve kesirler için a^(p/q) = (a^p)^(1/q). Her tanım temel işlemlerden ve fonksiyonlardan türetilir ve üsleme algebrada yüzlerce yıldır kullanılmıştır NCTM gibi eğitimciler tarafından etkilenmiş.
Türk eğitiminde üs hesaplayıcısı nasıl kullanılır?
Türk eğitim sisteminde bu üs hesaplayıcısı lise öğrencilerine algebrada üslemeyi pratik ettirir, MEB matematik müfredatıyla uyumlu olarak güç hesaplamalarını geliştirir.
Güç hesaplayıcısı Türkiye'de mühendislik sorunları için faydalı mı?
Evet, Türkiye'deki mühendisler güç hesaplayıcılarını yenilenebilir enerji projelerinde üstel büyümeyi modellemek için kullanır, üs yasalarını bilimsel veri hesaplamalarında hassas uygular.