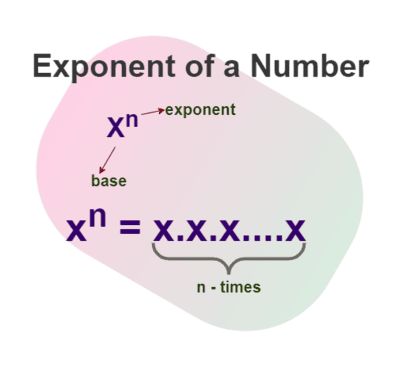Máy Tính Mũ
Xác định lũy thừa và mũ bằng công cụ trực tuyến này cho các phép lũy thừa chính xác.
📋Cách Sử Dụng Máy Tính Mũ?
-
Nhập số cơ số rõ ràng.
-
Nhập giá trị mũ tiếp theo.
-
Nhấn tính toán để có kết quả.
Bắt đầu sử dụng máy tính mũ bằng cách nhập cơ số hoặc số gốc vào ô đầu tiên; điều này sẽ đóng vai trò là số cơ số trong lũy thừa. Bây giờ nhập giá trị mũ chỉ ra số lần cơ số nên nhân với chính nó, là số nguyên dương, số âm hoặc thậm chí mũ phân số nếu phần phân số không phải là xấp xỉ sẽ thực hiện ở giai đoạn này. Nếu làm việc với ký hiệu khoa học hoặc dấu thập phân, hãy đảm bảo chọn đơn vị đo lường hoặc định dạng đúng. Khi hoàn tất, nhấn nút tính toán và nó sẽ tính toán đầu vào của bạn và trả về đầu ra.
Câu trả lời được đưa ra thường phản ánh giá trị đã tính cùng với các chi tiết khác liên quan đến đầu vào của bạn như biểu thức gốc được trả lại dưới thông tin cơ số đã tính. Ví dụ, nếu cơ số của một số là 2 và bạn nêu mũ là 5, nó sẽ đưa cho bạn câu trả lời đã tính là 32, (là bội số cơ bản của cơ số số).
Mẹo hữu ích💡
-
Kiểm tra mũ lớn với kiểm tra logarit để tránh tràn số.
-
Chuyển đổi phân số thành thập phân cho đầu vào lũy thừa phân số mượt mà hơn.
Mũ Được Tính Như Thế Nào
Số cơ số nâng lên mũ nghĩa là nhân lặp lại số cơ số với chính nó bao nhiêu lần được chỉ định bởi mũ. Đối với mũ số nguyên dương: 3^4 chỉ ra rằng 3 được nhân 4 lần, hoặc 3×3×3×3=81. Mũ số nguyên âm chỉ ra nghịch đảo: 2^-3=1/(2^3)=1/8. Mũ phân số chỉ ra căn và đại diện cho lũy thừa cũng vậy: 16^(1/2)=4 đại diện cho "căn bậc hai của 16." Máy tính sử dụng giá trị lớn với ước lượng logarit để tối đa hóa hiệu quả trong khi sản xuất kết quả chính xác đến các chữ số thập phân tiêu chuẩn. Các nguyên tắc được mô tả là các tiêu chuẩn được chấp nhận trong toán học, đã được xác nhận bởi các cơ quan toán học, và do đó, kết quả sẽ nhất quán qua các thực hành tính toán lũy thừa và lũy thừa.
Ứng Dụng Thực Tế📊
-
Đơn giản hóa biểu thức đại số trong bài tập hoặc kỳ thi.
-
Mô hình hóa tỷ lệ tăng trưởng trong tài chính sử dụng hàm lũy thừa.
-
Xác minh dữ liệu khoa học liên quan đến lũy thừa của mười.
Câu hỏi và Trả lời
Máy tính mũ là gì?
Máy tính mũ xác định hiệu quả kết quả của việc lấy một số đến mũ hoặc lũy thừa được chỉ định đại diện bởi số khác không phải cơ số. Nó làm việc với số nguyên, số âm và phân số để giải quyết vấn đề toán học nhanh chóng, hỗ trợ tính toán lũy thừa và lũy thừa.
Máy tính lũy thừa hoạt động như thế nào với mũ âm?
Máy tính lũy thừa vẫn xử lý mũ âm bằng cách lấy nghịch đảo của cơ số nâng lên mũ đó viết theo cách dương. Vậy nó xử lý 5^-2 giống như 1/25. Điều này hữu ích với vấn đề kiểu chia.
Tôi có thể sử dụng máy tính mũ cho toán học hàng ngày như thế nào?
Máy tính mũ là cách tiện lợi để đánh giá biểu thức toán học như 2^10, hoặc 3^4 như một phần của việc đơn giản hóa phương trình trong bối cảnh học thuật, hoặc các phần của toán học cơ bản, bao gồm các phép lũy thừa.
Tại sao chọn máy tính lũy thừa cho lũy thừa phân số?
Máy tính mũ đánh giá mũ phân số bằng cách kết hợp căn và nhân, ví dụ 8^(2/3)=4, giúp thực hiện các tính toán có vẻ phức tạp khi đánh giá căn.
Làm thế nào để tính 2 mũ 5 chính xác?
Để tính hai mũ năm, nhân hai với chính nó năm lần; tức là, 2×2×2×2×2=32, là phép nhân lặp lại đơn giản được thiết lập trong quy tắc số học cơ bản.
Máy tính với mũ có xử lý luật mũ không?
Và có, thậm chí máy tính mũ sử dụng quy tắc như nhân các cơ số giống nhau chỉ cộng mũ: (x^2)(x^3)=x^5, vậy chúng chỉ là cách tiện lợi để thực hiện tính toán đại số.
Công thức nào được sử dụng trong Máy Tính Mũ?
Máy tính mũ sử dụng phương trình lũy thừa cơ bản, a^b = a × a × a ×… (b lần), cho số nguyên dương, sau đó cho số nguyên âm, nó được định nghĩa a^(-b) = 1/(a^b), và cho phân số, a^(p/q) = (a^p)^(1/q). Mỗi định nghĩa được dẫn xuất từ các phép toán cơ bản và hàm nơi lũy thừa đã được sử dụng hàng trăm năm trong đại số ảnh hưởng bởi các nhóm giáo viên như National Council of Teachers of Mathematics (NCTM).
Máy tính mũ được sử dụng như thế nào trong giáo dục Việt Nam?
Trong hệ thống giáo dục Việt Nam, máy tính mũ này giúp học sinh THPT thực hành lũy thừa trong đại số, phù hợp với chương trình toán học của Bộ GD&ĐT để cải thiện tính toán lũy thừa.
Máy tính lũy thừa có hữu ích cho vấn đề kỹ thuật ở Việt Nam không?
Có, kỹ sư ở Việt Nam sử dụng máy tính lũy thừa để mô hình hóa tăng trưởng lũy thừa trong dự án xây dựng, áp dụng luật mũ vào các tính toán dữ liệu khoa học chính xác.