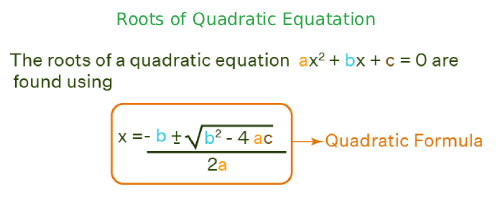Kök Hesap Makinesi

Kare kökleri, küp kökleri veya n'inci kökleri aracımızla hızlı belirleyin.

Kare Kök √
Küp Kök ∛
Genel Kök
4 √

Hesaplama Örnekleri

Hesaplama Durumu Sonuç
Karekök 144 12
Küpkök 27 3
625 sayısının 4. dereceden kökü 5

Kök Hesap Makinesini Nasıl Kullanırım?

Kök hesap makinesi kare kökler, küp kökleri ve daha yüksek dereceli kökler için hesaplamaları basit girişle gerçekleştirir. İlk olarak, kare kök, küp kök veya özel indeks için n'inci kök hesap makinesi gibi listeden bir kök türü seçin. Ardından kökünü belirlemek istediğiniz sayıyı girin, seçtiğiniz kök fonksiyonuyla tutarlı olmasına dikkat edin.

Örneğin, 16'nın kare kökünü hesaplamak için kare kök başlığı altında 16'yı girersiniz. Birimler sayısal giriş için standart kalır ve belirtilmedikçe girişi dönüştürmeniz gerekmez. Uygun sayıyı girdikten sonra hesapla düğmesine basın ve kök, tam kök değeri ve uygulanabilirse yaklaşık kök dahil sonuçları göreceksiniz. Bu süreç küp kökleri hesaplamak için benzerdir; 27 girerseniz cevap 3 olarak görünür, n'inci kök durumunda da öyledir; örneğin 81'in dördüncü kökü.

Kök hesap makinesi öncelikle pozitif gerçek sayılar için tasarlanmıştır ve karmaşık kök durumunda sinyal verir. Hesap makinesi eğitim amaçlı pratik uygulamalarda istenen hassasiyet derecesinde ondalık biçimde cevap hesaplayıp görüntüleme seçeneğine sahiptir.

Kök Hesaplamalarını Anlama

Kök hesaplamaları üs alma kurallarından yararlanır, burada bir sayı x'in kare kökü x üzeri 1/2 olarak yazılır, küp kök 1/3, n'inci kök 1/n, hepsi y^n = x formunda y'yi çözen denklemlerden türetilir. Mükemmel köklerle uğraşırken sonuçlar tam sayı olur, ancak çoğu kök bazı değeri yaklaşık verir - belirli ondalık nokta değerinde ilk belirtide, bu genellikle sonuçta yakınsamak için Newton-Raphson yöntemi gibi sayısal bir yöntem olarak uygulanan bazı hesaplama matematiği gerektirir. Araç, büyük ölçeğe ulaşan girişlerde verimlilik için bu yaklaşıklık süreçlerini uygular - gerektiğinde ondalık sayısını korur.İkinci dereceden denklemin kökleri

Uzman Tavsiyeleri 💡

  • Gerçek kök çıktıları için pozitif değerler girin; negatifler için karmaşık not edin.
  • Sonuçlarda kişiselleştirilmiş hassasiyet için ayarlar'da ondalık basamakları ayarlayın.

📋Hesaplama Adımları

  1. Kök türünü seçin (kare, küp veya n'inci).

  2. Hesaplanacak sayıyı girin.

  3. Anında kök sonucu için hesapla'ya tıklayın.

Kaçınılması Gereken Hatalar ⚠️

  1. Negatif sayıların çift dereceli köklerinin reel sayı olmadığını unutmak.
  2. Karekök ile küpök veya daha yüksek dereceli kökleri birbiriyle karıştırmak.
  3. Ara adımlarda ondalık sayıları çok erken yuvarlamak.
  4. Bir sayının karekökünün hem pozitif hem de negatif kökü olabileceğini atlamak.

Pratik Uygulamalar📊

  1. Geometri problemlerinde alan hesaplamaları için kare kökleri doğrulayın.

  2. Üç boyutlu şekiller için hacim hesaplamalarında küp kökleri değerlendirin.

  3. Polinom denklemleri doğru çözmek için cebirde n'inci kökleri keşfedin.

Sıkça Sorulan Sorular (SSS)

Kök hesap makinesi nedir?

Kök hesap makinesi sayılar için kare kök veya küp kök veya herhangi başka kök hesaplamak için önemli bir matematik kaynağıdır. Sonuç mükemmel kökler için tam olsun gibi 16'nın kare kökü 4'e eşittir veya 2'nin kare kökü gibi irrasyonel değerin kökü, doğru sonuçlar sağlayacaktır. Çevrimiçi kök hesap makinemiz basit kare kök hesaplamalarından daha gelişmiş kök bulmaya kadar izin verir ve diğer fonksiyonlar için hesaplamaları yaklaşıklar - cebirsel kullanım veya geometrik kullanım gibi diğer matematik süreçleriyle sorunlar için kullanılacak bütün matematik hesap makinesinin parçası olarak.

Kare kök nasıl hesaplanır?

Kare kökü bulmak için amaç, kendisiyle çarpıldığında orijinal sayıya eşit olan sayıyı bulmaktır - y² = x'i çözmekle aynı. Kare kök hesap makineniz varsa, sayıyı kare kök hesap makinesine girerdiniz ve o sizin için hesaplamaları yapardı, tabii ki işi görmek isterseniz o da mevcuttu. Örneğin, 8'in kare kökü 2√2'ye indirgenir - günlük matematik hesaplamaları veya hassas mühendislik tahminleri için hızlı uygulamalarda daha kullanışlıdır.

Küp kök hesap makinesi ne için kullanılır?

Küp kök hesap makinesi küplendiğinde girişi veren sayıyı tanımlar - üç boyutlu şekillerin hacmini bulmak veya cebirde polinom denklemleri çözmek için önemlidir. 27'nin küp kökünü bulabilir - 3 bulur veya 12'nin küp kökü gibi küp olmayan birini yaklaşıklar. Hesap makinesi küp kök sembolü bulmak ve küp kök notasyonu hesaplamak gibi ilgili fonksiyonları da gerçekleştirir. Hesap makinesi uzamsal ilişkilerle uğraşan veya polinomlarla kök çözümü yapan herhangi bir durumda çok kullanışlıdır.

N'inci kök nasıl bulunur?

N'inci kökü bulmak için kök indeksi n ve radicand tanımlamalısınız, sonra çıktı (1/n) kuvvetine yükseltilmiş sayıdır veya y^n = x gibi bir denklem çözmektir. N'inci kök hesap makinesi n'inci köklerinizi bulmayı daha verimli kılar - kendi indeksinizi ayarlama yeteneğiyle, geometride dördüncü kökler, havada ayaklar veya matematikte daha yüksek dereceli hesaplanmış kökler olsun. N'inci kök hesap makinesi n'inci kökleri değerlendirmek veya kök formüllerini değerlendirmek için kullanışlı tam kök değeri çıktıları verir ve kökler gerçek veya yaklaşık olsun istenildiğinde hassasiyetin korunduğundan emin olur.

Negatif sayıların kare kökü ne olacak?

Negatif sayıların kare kökü, -9'un kare kökü gibi, gerçek sayılar negatiflerin çift köklerine sahip olmadığından 3i gibi hayali sonuçlar verir. Tam kök hesap makinesi bu durumları bulur, değerlendirir ve karmaşık kökleri açıklamaya yardımcı olur - karmaşık kare köklerle yardım için bağlantılar sağlar. Bu, daha temel gerçek kök ölçümlerinden daha gelişmiş konulara geçen öğrenciler için kullanışlıdır - karmaşık analize geçiş veya hatta fizik simülasyonları gibi.

Kök hesap makinesi büyük sayıları işleyebilir mi?

Evet, sağlam bir kök hesap makinesi büyük sayıları etkili yönetir - Newton-Raphson gibi yinelemeli yöntemler kullanarak geniş girişlerin kare köklerinde, küp köklerinde veya n'inci köklerinde yakınsama sağlar. Hesaplama sınırlarına kadar değerleri işler - ayarlanabilir hassasiyetle ondalık yaklaşıklıklar sunar - büyük tamsayıların kare kökü veya mühendislikte hacimlerin küp kökü içeren bilimsel hesaplamalar için ideal. Bu yetenek yüksek hacimli veriler için kök hesap makinesi varyantlarına uzanır - güvenilirlik kaybı olmadan.

Kök hesap makinesinde hangi formüller kullanılır?

Kök hesap makinesi temel üs alma formüllerine dayanır: kare kök √x veya x^(1/2) olarak gösterilir, küp kök ∛x veya x^(1/3), genel n'inci kök ⁿ√x veya x^(1/n). Bunlar radikal denklemleri çözmek için cebirsel ilkelerden türetilir ve American Mathematical Society ile International Mathematical Union standartlarıyla doğrulanır - kök çarpımı veya formül tabanlı türetmeler gibi görevler için gerçek ve karmaşık alanlarda tutarlı doğruluk sağlar.

🔢Daha Fazla Hesap Makinesi Deneyin

Kare Formülü Hesap Makinesi
Çarpan Hesaplayıcı
Z-Skor Hesaplayıcı
Not: Bu hesaplayıcı, bilgilendirme amaçlı faydalı tahminler sunmak için tasarlanmıştır. Doğruluk için çaba göstersek de sonuçlar yerel yasalara ve bireysel durumlara göre değişiklik gösterebilir. Önemli kararlar için profesyonel bir danışmana başvurmanızı öneririz.