Root Calculator
Determine square roots, cube roots, or nth roots quickly wit our tool.
📋How to Use Root Calculator?
-
Select root type (square, cube, or nth).
-
Enter the number to compute.
-
Click calculate for instant root result.
The root calculator performs calculations for square roots, cube roots, and higher-order roots through simple entry. First, select a root type from the list such as the square root, cube root, or the nth root calculator for a custom index. Then you may enter the number for which you would like to determine the root, keeping in mind that it should be consistent with the root function you selected.
For example, to calculate the square root of 16, you would simply enter 16 under the square root heading. The units remain standard for numerical entry, and does not require you to convert the entry unless specified. After entering the appropriate number, simply press the calculate button, and you will see the results which include the root, the exact root value, and the approximated root, if applicable. This process is similar for calculating cube roots; if you enter 27 you will see the answer as 3, as well as in the case for the nth root; for example, the fourth root of 81.
The root calculator is designed for primarily positive real numbers and will signal in the case of a complex root. The calculator features the option to calculate and display an answer in decimal form to the desired degree of precision for educational uses in practical applications.
Useful Tips💡
-
Input positive values for real root outputs; note complex for negatives.
-
Adjust decimal places in settings for tailored precision in results.
Understanding Root Calculations
Root calculations draw on exponentiation rules, where the square root of a number x is written x raised to 1/2, cube root 1/3, nth root 1/n, which are all derived from equations that solve for y in the form of y^n = x. When dealing with perfect roots the results are an integer, however most roots will approximate some value giving you to a set decimal point value at some first indication, this often requires some computational math normally implemented as a numerical method, e.g., Newton-Raphson method to converge on the result. The tool implements these approximation processes for efficiency with operation on inputs that reach large scale while preserving the number of decimals as needed.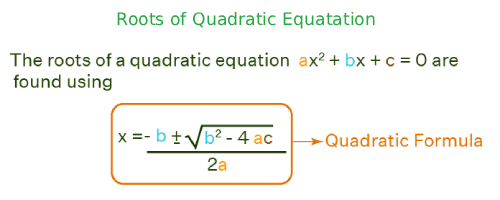
Practical Applications📊
-
Verify square roots in geometry problems for area computations.
-
Assess cube roots in volume calculations for three-dimensional shapes.
-
Explore nth roots in algebra to solve polynomial equations accurately.
Questions and Answers
What is a root calculator?
A root calculator is an important math resource for computing square roots or cube roots or any other roots of numbers. Whether the result is exact for perfect roots like the square root of 16 is equal to 4 or the root of an irrational value like square root of 2, it will provide accurate results. Our online root calc allows for simple square root calculations to more advanced root finding, and it approximates calculations for other functions as a part of the whole math calculator to be used for problems with other math processes such as algebraic use or geometric use.
How to calculate square root?
To find the square root, the goal is to find the number that, when multiplied by itself equals the original number, the same as solving for y² = x. If you have a square root calculator, you would input the number into the square root calculator, and it would do the calculations for you, unless of course you wanted to see the work, which was also available. For example, the square root of 8 is reduced to 2√2, which is more useful for rapid applications for daily mathematical computations or precise engineering estimates.
What is cube root calculator used for?
A cube root calculator identifies the number that yields the input when cubed, which is significant for finding volume of three-dimensional shapes or finding polynomial equations in algebra. It can find a cube root of 27, which would find 3 or approximate a non-cube such as the cube root of 12. The calculator will also perform related functions such as finding a cube root symbol and computing a cubed root notation. The calculator is very useful in any instance dealing with spatial relationships or root solving with polynomials.
How to find nth root?
To find the nth root, you will have to define the root index n and the radicand, then the output is the number to the power of (1/n), or solving an equation like y^n = x. The nth root calculator makes finding your nth roots more efficient, with the ability to set your own index, whether fourth roots in geometry, feet in air, or calculated roots of higher order in mathematics. The nth root calculator will give you exact root value outputs useful to evaluate nth roots or root formulas, and make certain that accuracy is preserved when requested regardless of whether the roots are real or approximated.
What about square root of negative numbers?
The square root of negative numbers, like the square root of -9, gives us imaginary results, like 3i, because real numbers do not have even roots of negatives. A full root calculator will find these cases, evaluate and help to explain complex roots, and provide links to help with complex square roots. This is helpful for students transitioning from more basic real root measurements to studying more advanced topics, like transitioning into complex analysis, or even to physics simulations.
Can root calculator handle large numbers?
Yes, a robust root calculator manages large numbers effectively, employing iterative methods like Newton-Raphson for convergence on square roots, cube roots, or nth roots of extensive inputs. It processes values up to computational limits, delivering decimal approximations with adjustable precision—ideal for scientific computations involving square root of large integers or cube root of volumes in engineering. This capability extends to roots calculator variants for high-volume data without loss of reliability.
What formulas are used in the root calculator?
The root calculator relies on fundamental exponentiation formulas: square root denoted as √x or x^(1/2), cube root as ∛x or x^(1/3), and general nth root as ⁿ√x or x^(1/n). These derive from algebraic principles for solving radical equations and are verified by standards from the American Mathematical Society and the International Mathematical Union, ensuring consistent accuracy in real and complex domains for tasks like root multiplication or formula-based derivations in advanced math.