Z-Skor Hesaplayıcı

Herhangi bir veri noktasının normal dağılımdaki standartlaştırılmış konumunu belirleyin.

Z-skor: —

Z-skor ↔ Olasılık Dönüştürücü

P(x < Z)
—
P(x > Z)
—
P(0 < x < Z)
—
P(-Z < x < Z)
—
P(x < -Z veya x > Z)
—

Hesaplama Örnekleri

Hesaplama Durumu Sonuç
Değer: 85, Ortalama: 70, S. Sapma: 10 Z-skoru = 1,5
Ortalamanın altındaki bir değer için z-skoru Negatif (-) sonuç
Standart normal dağılım tablosu kullanımı Olasılık değerine dönüştürme

Z-Skor Hesaplayıcı Nasıl Kullanılır?

Sadece üç giriş gerekir. Gözlemlenen ham puanı (analiz ettiğiniz veri noktası) girin. Ardından referans aldığınız dağılımın popülasyon ortalamasını – aritmetik ortalamayı – belirtin. Son olarak aynı popülasyonun standart sapmasını girin. Üç alan doldurulduktan sonra “Hesapla”ya basın. Sonuç hemen z-skor olarak görünür ve ham puanın ortalamanın kaç standart sapma üstünde (pozitif) veya altında (negatif) olduğunu gösterir.

Z-Skor Nasıl Hesaplanır

Z-skor – standart skor olarak da bilinir – ham puandan popülasyon ortalaması çıkarılarak ve fark popülasyon standart sapmasına bölünerek elde edilir. Elde edilen değer orijinal gözlemi standart normal dağılıma (ortalama = 0, standart sapma = 1) yerleştirir ve olasılık hesaplamalarını ve istatistiksel karşılaştırmaları kolaylaştırır.Z-tablosu

Uzman Tavsiyeleri 💡

  • Popülasyon parametreleri biliniyorsa kullanın; örnek veri için z-skor yerine t-skor düşünün
  • Normal dağılımlı verilerde |z| > 3 değerleri genellikle olağandışı veya potansiyel aykırı değer kabul edilir

📋Hesaplama Adımları

  1. Ham puanı (gözlemlenen değeri) girin

  2. Popülasyon ortalamasını (μ) girin

  3. Popülasyon standart sapmasını (σ) girin

Kaçınılması Gereken Hatalar ⚠️

  1. Evren (popülasyon) yerine örneklem standart sapmasını kullanmak.
  2. Standart sapmaya bölmeden önce ortalamayı çıkarmayı unutmak.
  3. Z-skorunun 3'ten büyük olamayacağını sanmak (nadirdir ama mümkündür).
  4. Z-skoru değeri ile tablodaki olasılık (p-değeri) değerini karıştırmak.

Pratik Kullanım Alanları📊

  1. Sınav puanlarını (SAT, GRE, IQ) farklı versiyonlar arasında adil karşılaştırma için standartlaştırma

  2. Araştırma veri setlerinde ve kalite kontrol izlemede aykırı değer tespiti

  3. Normal dağılımlı değişkenlerde olasılık ve yüzdelik hesaplama

Sıkça Sorulan Sorular (SSS)

İstatistikte z-skor nedir?

Z-skor, ham puanın popülasyon ortalamasından uzaklığını popülasyon standart sapması birimleriyle ifade eder. Herhangi bir normal dağılımı standart normal dağılıma dönüştürerek standart tabloların ve olasılık hesaplarının kullanılmasını sağlar.

Z-skoru elle nasıl hesaplanır?

Ham puandan popülasyon ortalaması çıkarılır ve sonuç popülasyon standart sapmasına bölünür. Popülasyon parametreleri bilindiğinde evrensel formül z = (x − μ) / σ kullanılır. Çevrimiçi hesaplayıcılar bu işlemi anında yapar ve aritmetik hataları ortadan kaldırır.

Ortalama ve standart sapma biliniyorsa z-skor nasıl bulunur?

Ham puan (x), popülasyon ortalaması (μ) ve popülasyon standart sapması (σ) biliniyorsa doğrudan z-skor formülüne yerleştirilir ve standartlaştırılmış değer elde edilir. Bu yaklaşım çıkarımsal istatistik ve hipotez testlerinde standarttır.

Negatif z-skor neyi gösterir?

Negatif standart skor, veri noktasının popülasyon ortalamasının altında olduğunu gösterir. Örneğin −1.5 z-skoru, değerin dağılım ortalamasının 1.5 standart sapma altında olduğunu belirtir.

Z-skor olasılık bulmak için nasıl kullanılır?

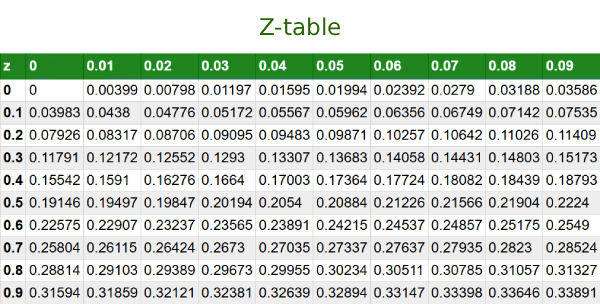
Z-skor elde edildikten sonra standart normal dağılım tablosu (z-tablosu) veya birikimli dağılım fonksiyonu kullanılarak eğri altındaki alan belirlenir. Bu alan, standartlaştırılmış skordan küçük veya eşit değer gözleme olasılığına karşılık gelir.

Bu z-skor hesaplayıcı hangi formülü kullanır?

Hesaplayıcı dünya çapında kabul görmüş standart z-skor formülünü kullanır: z = (x − μ) / σ, burada x ham puan, μ popülasyon ortalaması ve σ popülasyon standart sapmasıdır. 20. yüzyılın başında formalize edilen ve Royal Statistical Society ile American Statistical Association tarafından onaylanan bu formül, normal dağılım analizlerinde standartlaştırmanın temel taşıdır.

Z-skor sonuçları nasıl yorumlanır?

Z-skor 0 gözlemi tam popülasyon ortalamasına yerleştirir. Normal dağılımda verilerin yaklaşık %68’i ±1, %95’i ±2 ve %99.7’si ±3 standart sapma içinde yer alır. Mutlak değeri büyük z-skorlar, verilen popülasyona göre giderek daha nadir gözlemleri gösterir.

🔢Daha Fazla Hesap Makinesi Deneyin

Kalan Hesaplama Makinesi
Hex Hesap Makinesi
Yüzde Hesaplama Makinesi
Not: Bu hesaplayıcı, bilgilendirme amaçlı faydalı tahminler sunmak için tasarlanmıştır. Doğruluk için çaba göstersek de sonuçlar yerel yasalara ve bireysel durumlara göre değişiklik gösterebilir. Önemli kararlar için profesyonel bir danışmana başvurmanızı öneririz.