Calculateur de Z-Score

Déterminez la position standardisée de n’importe quel point de données dans une distribution normale.

Z-score : —

Convertisseur Z-score ↔ Probabilité

P(x < Z)
—
P(x > Z)
—
P(0 < x < Z)
—
P(-Z < x < Z)
—
P(x < -Z ou x > Z)
—

Exemples de calcul

Cas de calcul Résultat
Score 115, Moyenne 100, Écart-type 15 Z-score = 1
Position d'une donnée dans une loi normale Interprétation statistique
Calcul de la probabilité associée au score Z Usage en psychométrie et tests

Comment utiliser le Calculateur de Z-Score ?

Trois entrées suffisent. Saisissez la valeur brute observée (le point de données analysé). Indiquez ensuite la moyenne de la population – la moyenne arithmétique de toute la distribution de référence. Enfin, entrez l’écart-type de la population – mesure de dispersion de cette même population. Une fois les trois champs remplis, cliquez sur « Calculer ». Le résultat apparaît immédiatement sous forme de z-score, indiquant de combien d’écarts-types la valeur est au-dessus (positif) ou en dessous (négatif) de la moyenne.

Comment le Z-Score est-il calculé

Le z-score – ou score standard – s’obtient en soustrayant la moyenne de la population à la valeur brute, puis en divisant la différence par l’écart-type de la population. La valeur obtenue place l’observation initiale sur la distribution normale standard (moyenne = 0, écart-type = 1), ce qui simplifie les calculs de probabilité et les comparaisons statistiques.Table Z

Conseils d’Experts 💡

  • Utilisez les paramètres de population lorsqu’ils sont connus ; pour des données d’échantillon, préférez le t-score
  • Les valeurs dont |z| > 3 sont généralement considérées comme inhabituelles ou potentiellement aberrantes dans une distribution normale

📋Étapes de calcul

  1. Saisissez la valeur brute observée

  2. Saisissez la moyenne de la population (μ)

  3. Saisissez l’écart-type de la population (σ)

Erreurs à éviter ⚠️

  1. Utiliser l'écart-type de l'échantillon au lieu de celui de la population.
  2. Oublier de soustraire la moyenne avant de diviser par l'écart-type.
  3. Penser qu'un score Z supérieur à 3 est impossible (rare mais possible).
  4. Confondre le score Z avec la valeur de probabilité (p-value) de la table.

Applications pratiques📊

  1. Standardiser les scores de tests (SAT, GRE, QI) pour une comparaison équitable entre différentes versions

  2. Détecter les valeurs aberrantes dans les jeux de données de recherche et le contrôle qualité

  3. Calculer des probabilités et des percentiles pour des variables normalement distribuées

Questions Fréquentes (FAQ)

Qu’est-ce qu’un z-score en statistique ?

Un z-score représente la distance d’une valeur brute par rapport à la moyenne de la population, exprimée en unités d’écart-type de la population. Il transforme toute distribution normale en distribution normale standard, permettant l’utilisation de tables standardisées et de calculs de probabilité.

Comment calculer un z-score manuellement ?

Soustrayez la moyenne de la population à la valeur observée et divisez le résultat par l’écart-type de la population. La formule universelle est z = (x − μ) / σ quand les paramètres de population sont connus. Les calculateurs en ligne effectuent cette opération instantanément et éliminent les erreurs arithmétiques.

Comment trouver un z-score quand la moyenne et l’écart-type sont connus ?

Avec la valeur brute (x), la moyenne de la population (μ) et l’écart-type de la population (σ), il suffit de remplacer dans la formule du z-score pour obtenir la valeur standardisée. Cette méthode est classique en statistique inférentielle et dans les tests d’hypothèses.

Que signifie un z-score négatif ?

Un score standard négatif indique que le point de données se situe en dessous de la moyenne de la population. Par exemple, un z-score de −1.5 signifie que la valeur est à 1.5 écart-type en dessous de la moyenne de la distribution.

Comment utiliser le z-score pour trouver une probabilité ?

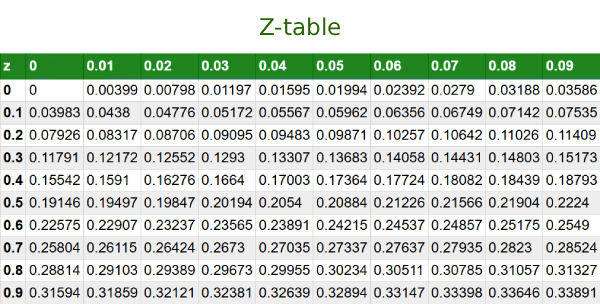
Après avoir obtenu le z-score, consultez la table de la distribution normale standard (table Z) ou la fonction de répartition pour déterminer l’aire sous la courbe. Cette aire correspond à la probabilité d’observer une valeur inférieure ou égale au score standardisé.

Quelle formule utilise ce calculateur de z-score ?

Le calculateur applique la formule standard mondialement reconnue : z = (x − μ) / σ, où x est la valeur brute, μ la moyenne de la population et σ l’écart-type de la population. Formalisée au début du XXe siècle et approuvée par la Royal Statistical Society et l’American Statistical Association, elle reste la pierre angulaire de la standardisation dans l’analyse de la distribution normale.

Comment interpréter les résultats d’un z-score ?

Un z-score de 0 place l’observation exactement à la moyenne de la population. Environ 68 % des données se trouvent dans ±1, 95 % dans ±2 et 99.7 % dans ±3 écarts-types dans une distribution normale. Des valeurs absolues plus élevées indiquent des observations de plus en plus rares par rapport à la population donnée.

🔢Outils Recommandés

Calculateur de Reste
Calculatrice Hexadécimale
Calculatrice de Pourcentage
Note : Ce calculateur est conçu pour fournir des estimations utiles à des fins d'information. Bien que nous fassions tout notre possible pour garantir l'exactitude, les résultats peuvent varier en fonction des lois locales et des circonstances individuelles. Nous vous recommandons de consulter un conseiller professionnel pour toute décision importante.