Calculadora de Z-Score

Determina la posición estandarizada de cualquier punto de datos dentro de una distribución normal.

Z-score: —

Convertidor Z-score ↔ Probabilidad

P(x < Z)
—
P(x > Z)
—
P(0 < x < Z)
—
P(-Z < x < Z)
—
P(x < -Z o x > Z)
—

Ejemplos de cálculo

Caso de cálculo Resultado
Valor 85, Media 70, DE 10 1,5
Valor 50, Media 60, DE 5 -2,0
Cuando el valor es igual a la media 0

¿Cómo usar la Calculadora de Z-Score?

Solo necesitas tres datos. Introduce el valor bruto observado (el punto de datos que estás analizando). Luego indica la media poblacional - el promedio aritmético de toda la distribución de referencia. Finalmente, ingresa la desviación estándar poblacional - la medida de dispersión de esa misma población. Al completar los tres campos y pulsar “Calcular”, el resultado aparece al instante como z-score, indicando cuántas desviaciones estándar está el valor por encima (positivo) o por debajo (negativo) de la media.

Cómo se calcula el Z-Score

El z-score - también llamado puntaje estándar - se obtiene restando la media poblacional al valor bruto y dividiendo la diferencia entre la desviación estándar poblacional. El valor resultante coloca la observación original en la distribución normal estándar (media = 0, desviación estándar = 1), lo que simplifica los cálculos de probabilidad y las comparaciones estadísticas.Tabla Z

Guía de Uso y Consejos 💡

  • Usa parámetros poblacionales cuando se conocen; para datos muestrales considera un t-score en lugar de z-score
  • Valores con |z| > 3 suelen considerarse inusuales o posibles valores atípicos en datos con distribución normal

📋Pasos para Calcular

  1. Introduce el valor bruto observado

  2. Introduce la media poblacional (μ)

  3. Introduce la desviación estándar poblacional (σ)

Errores a evitar ⚠️

  1. Usar la desviación estándar de la muestra cuando se requiere la de la población.
  2. Olvidar restar la media aritmética antes de dividir por la desviación estándar.
  3. Creer que un Z-score mayor a 3 es imposible (es poco común, pero ocurre).
  4. Confundir la puntuación Z con el valor de probabilidad (valor p) en la tabla.

Aplicaciones prácticas📊

  1. Estandarizar puntuaciones de exámenes (SAT, GRE, IQ) para comparar versiones diferentes de forma justa

  2. Detectar valores atípicos en conjuntos de datos de investigación y control de calidad

  3. Calcular probabilidades y percentiles en variables con distribución normal

Preguntas Frecuentes (FAQ)

¿Qué es un z-score en estadística?

Un z-score representa la distancia de un valor bruto respecto a la media poblacional expresada en unidades de la desviación estándar poblacional. Transforma cualquier distribución normal en la distribución normal estándar, permitiendo usar tablas estandarizadas y cálculos de probabilidad.

¿Cómo calcular manualmente un z-score?

Resta la media poblacional al valor observado y divide el resultado entre la desviación estándar poblacional. La fórmula universal es z = (x − μ) / σ cuando se conocen los parámetros poblacionales. Las calculadoras online realizan esta operación al instante y eliminan errores aritméticos.

¿Cómo hallar el z-score cuando se conocen media y desviación estándar?

Con el valor bruto (x), la media poblacional (μ) y la desviación estándar poblacional (σ), basta sustituir directamente en la fórmula del z-score para obtener el valor estandarizado. Este enfoque es estándar en estadística inferencial y pruebas de hipótesis.

¿Qué indica un z-score negativo?

Un puntaje estándar negativo indica que el punto de datos original está por debajo de la media poblacional. Por ejemplo, un z-score de −1.5 significa que el valor está 1.5 desviaciones estándar por debajo del promedio de la distribución.

¿Cómo se usa el z-score para encontrar probabilidades?

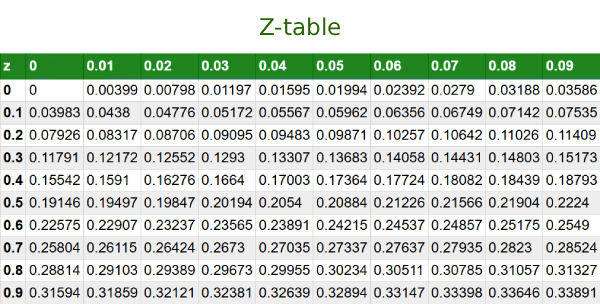
Una vez obtenido el z-score, consulta la tabla de la distribución normal estándar (tabla Z) o la función de distribución acumulativa para determinar el área bajo la curva. Esa área corresponde a la probabilidad de observar un valor menor o igual al puntaje estandarizado.

¿Qué fórmula utiliza esta calculadora de z-score?

La calculadora aplica la fórmula estándar de z-score reconocida mundialmente: z = (x − μ) / σ, donde x es el valor bruto, μ la media poblacional y σ la desviación estándar poblacional. Esta fórmula, formalizada a principios del siglo XX y respaldada por la Royal Statistical Society y la American Statistical Association, sigue siendo la base de la estandarización en análisis de distribución normal.

¿Cómo interpretar los resultados del z-score?

Un z-score de 0 sitúa la observación exactamente en la media poblacional. Aproximadamente el 68% de los datos caen dentro de ±1, el 95% dentro de ±2 y el 99.7% dentro de ±3 desviaciones estándar en una distribución normal. Valores absolutos mayores indican observaciones cada vez más raras respecto a la población dada.

🔢Otras herramientas que podrían interesarte

Calculadora de Residuo
Calculadora Hexadecimal
Calculadora de Porcentajes y Variaciones
Nota: Esta calculadora está diseñada para ofrecer estimaciones útiles con fines informativos. Aunque nos esforzamos por la precisión, los resultados pueden variar según las leyes locales y las circunstancias individuales. Recomendamos consultar con un asesor profesional para decisiones importantes.