Calculadora Hexadecimal
Gestione la aritmética hexadecimal y convierta entre números decimales y hexadecimales con total precisión.
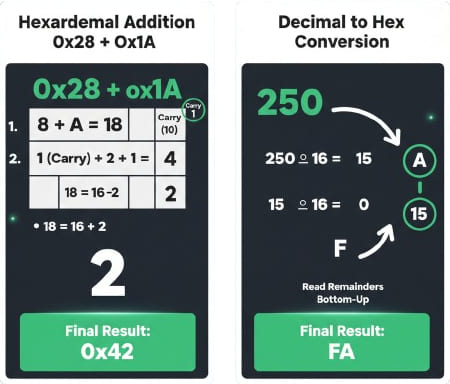
Ejemplos de cálculo
¿Cómo usar la calculadora hexadecimal?
Para utilizar esta calculadora hex, comience introduciendo su valor en el campo de entrada principal. Nuestra herramienta está diseñada para manejar tanto la suma hexadecimal como la resta hexadecimal de forma sencilla y rápida. Simplemente proporcione el primer número (usando dígitos del 0-9 y letras de la A-F) y seleccione la operación deseada. Para tareas aritméticas avanzadas como el uso de un multiplicador hex o la realización de una división hex, introduzca el segundo valor y haga clic en "Calcular".
Esta calculadora hex online también funciona como un potente conversor hexadecimal. Si necesita realizar una transformación de hex a decimal o de decimal a hex, solo tiene que introducir un valor único. La herramienta mostrará automáticamente el resultado en ambos sistemas numéricos de forma instantánea. Es una calculadora de base 16 esencial para profesionales y estudiantes que trabajan con direcciones de memoria, operaciones de bits o códigos de color HTML/CSS.
Cómo se realizan las operaciones y conversiones hexadecimales
Esta calculadora matemática hex funciona según el principio posicional de la base 16. A diferencia del sistema decimal convencional (base 10), el sistema hexadecimal utiliza dieciséis símbolos distintos (0-9 y A-F). El valor de cualquier número se calcula mediante la fórmula matemática: $N = \sum_{i=0}^{n} d_i \times 16^i$.
Para la suma hexadecimal, sumamos los dígitos columna por columna de derecha a izquierda. Si la suma de una columna supera 15, realizamos un acarreo (carry) de 1 hacia la siguiente posición (que representa un valor de 16 en decimal). En la resta, realizamos un préstamo (borrow) de 16 de la columna siguiente si el dígito del minuendo es menor que el sustraendo. Para la conversión a decimal, cada dígito se multiplica por su potencia correspondiente de 16. Por el contrario, convertir decimal a hex implica la división repetida por 16, registrando los residuos como dígitos hexadecimales en orden inverso.
Guía de Uso y Consejos 💡
- Utilice letras A-F en mayúsculas para cumplir con las convenciones estándar de documentación técnica.
- Revise la salida decimal secundaria para validar sus cálculos manuales y evitar errores de lógica.
- Para conversiones de base simples, use la herramienta como un conversor hex dedicado proporcionando una sola entrada.
📋Pasos para Calcular
-
Introduzca el primer número en formato hexadecimal (0-F) o decimal.
-
Seleccione la operación aritmética (+, -, *, /) o déjelo en blanco para una conversión directa.
-
Haga clic en el botón Calcular para obtener los resultados detallados en ambos sistemas.
Errores a evitar ⚠️
- Intentar usar caracteres fuera del rango permitido (como las letras G, H o Z).
- Aplicar erróneamente las reglas de acarreo de base 10 (en lugar de base 16) durante sumas manuales.
- Invertir accidentalmente el orden de los restos al realizar la conversión de decimal a hex a mano.
- Ignorar el contexto del sistema de complemento a dos al trabajar con números hexadecimales con signo.
Aplicaciones Prácticas📊
Cálculo de offsets de memoria y direcciones de punteros en programación de bajo nivel (C, C++, Assembly).
Conversión de valores RGB a códigos de colores hexadecimales para diseño web moderno.
Verificación de operaciones bit a bit (bitwise) y codificación de datos en ciencias de la computación.
Depuración de firmware mediante comprobaciones rápidas de conversión de hex a entero (hex to integer).