Calculadora Hexadecimal

Manipule aritmética hexadecimal e converta entre números decimais e hexadecimais com total precisão.

Calculadora Hex
Decimal → Hex
Hex → Decimal

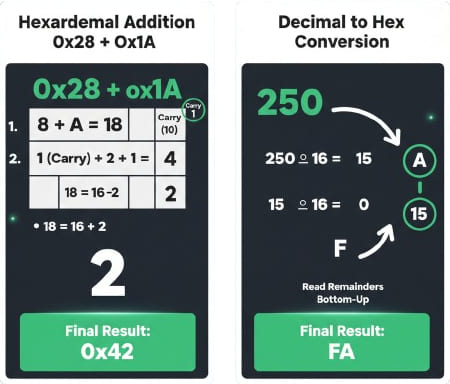
Exemplos de Cálculo

Caso de Cálculo Resultado
Soma Hex: 0xA + 0x5 0xF (Decimal: 15)
Hex para Decimal: 0xFF 255
Decimal para Hex: 1000 0x3E8
Subtração Hex: 0x20 - 0x1 0x1F (Decimal: 31)

Como usar a calculadora hexadecimal?

Para utilizar esta calculadora hex, comece inserindo seu valor no campo de entrada principal. Nossa ferramenta foi desenvolvida para processar tanto a soma hexadecimal quanto a subtração hexadecimal de forma intuitiva. Basta fornecer o primeiro número (usando dígitos de 0-9 e letras de A-F) e selecionar a operação desejada. Para tarefas aritméticas como multiplicação ou divisão hex, insira o segundo valor e clique em "Calcular".

Esta calculadora online também atua como um poderoso conversor hexadecimal. Se precisar transformar hex em decimal ou decimal em hex, basta inserir um único valor. É uma ferramenta de base 16 indispensável para programadores que trabalham com endereçamento de memória, operações bitwise ou códigos de cores HTML/CSS, garantindo resultados instantâneos.

Como são realizadas a aritmética e as conversões hexadecimais

Esta calculadora opera com base no princípio posicional da base-16. Ao contrário do sistema decimal comum (base 10), o hexadecimal utiliza dezesseis símbolos (0-9 e A-F). O valor numérico é calculado pela fórmula matemática: $N = \sum_{i=0}^{n} d_i \times 16^i$.

Na adição hexadecimal, somamos os dígitos coluna por coluna. Se a soma de uma coluna exceder 15, fazemos o carry over (transporte) de 1 para a próxima posição à esquerda. Na subtração, realizamos o borrow (empréstimo) de 16 da coluna vizinha se o dígito for menor que o subtraendo. Para a conversão decimal, cada dígito é multiplicado pela sua respectiva potência de 16. Já a conversão de decimal para hex envolve divisões sucessivas por 16, onde os restos são anotados como dígitos hexadecimais.

Exemplo de soma e conversão hexadecimal

Dicas Úteis 💡

  • Utilize letras A-F em maiúsculas para seguir as convenções padrão da indústria de software.
  • Sempre verifique a saída decimal para validar cálculos manuais complexos.
  • Para conversões rápidas de base, forneça apenas um valor de entrada para ativar o modo conversor.

📋Passos para Calcular

  1. Insira o primeiro número no formato hexadecimal (0-F) ou decimal.

  2. Selecione a operação aritmética ou deixe o campo em branco para uma conversão simples.

  3. Clique em Calcular para visualizar os resultados detalhados em ambos os sistemas numéricos.

Erros a evitar ⚠️

  1. Tentar utilizar caracteres inválidos como G, H ou Z no sistema hexadecimal.
  2. Aplicar regras de transporte de base 10 (carry aos 10) em vez das regras de base 16.
  3. Inverter a ordem dos restos ao converter manualmente de decimal para hex.
  4. Desconsiderar o contexto de complemento de dois ao lidar com aritmética hexadecimal assinada.

Aplicações Práticas📊

  1. Cálculo de offsets de memória e endereços de ponteiros em linguagens de baixo nível como C e Assembly.

  2. Conversão de valores RGB para códigos hexadecimais de cores em desenvolvimento web.

  3. Verificação de operações lógicas bitwise e codificação de dados em sistemas digitais.

  4. Realização de checagens rápidas de hex para inteiro (hex to integer) durante o debugging de firmware.

Perguntas e Respostas

O que é uma calculadora hexadecimal e para que serve?

Uma calculadora hexadecimal é uma ferramenta técnica projetada para realizar operações aritméticas — como soma, subtração, multiplicação e divisão — diretamente na base 16. Além das operações matemáticas, ela funciona como uma ponte entre sistemas, permitindo a conversão de valores hex para decimal e vice-versa. Isso é vital na computação, onde o sistema hex é usado para representar endereços de memória, códigos de cores e fluxos de dados binários de forma mais compacta que o sistema decimal.

Como funciona a soma hexadecimal com transporte (carry)?

A soma hexadecimal segue uma lógica de colunas semelhante à decimal, mas com limite de 16. Você soma os dígitos de uma coluna; se o resultado for 15 ou menos, escreve-se o dígito (usando A-F para 10-15). Se a soma for 16 ou mais, subtrai-se 16 do total, escreve-se o resto e faz-se o transporte (carry) de 1 para a próxima coluna à esquerda. Por exemplo, $F + 1$ resulta em $0$ com transporte de $1$, escrito como $10_{16}$ (que equivale a 16 em decimal).

Qual o método para converter decimal para hexadecimal?

Para converter um número decimal para hex, utiliza-se o método de divisão repetida por 16. Divide-se o número inteiro por 16 e anota-se o resto da divisão. Continua-se dividindo o quociente por 16 até que ele chegue a zero. Os restos obtidos (convertidos para os dígitos hex 0-F) são lidos na ordem inversa (do último para o primeiro). Por exemplo, o decimal 250 torna-se $FA_{16}$ após este processo.

Como converter um valor hexadecimal para decimal manualmente?

A conversão de hex para decimal envolve multiplicar cada dígito hexadecimal por 16 elevado à potência da sua posição, começando da direita para a esquerda (posição 0). Por exemplo, para converter $2B$: $(2 \times 16^1) + (11 \times 16^0) = 32 + 11 = 43$. Este método de soma posicional permite traduzir com precisão qualquer string hexadecimal em um número decimal inteiro.

Por que o sistema hexadecimal é tão usado na programação?

O hexadecimal é o padrão na programação porque oferece uma forma legível de representar dados binários. Como $16$ é $2^4$, exatamente um dígito hex representa quatro bits (um "nibble"). Isso facilita muito o gerenciamento de strings binárias longas; por exemplo, um byte de 8 bits pode ser escrito com apenas dois dígitos hex (00 a FF). É o formato preferido para definir cores RGB, endereços de memória e protocolos de rede.

Quais fórmulas a calculadora utiliza para garantir precisão?

Nossa ferramenta aplica a fórmula fundamental de notação posicional: $Valor = \sum_{i=0}^{n} (d_i \times 16^i)$, onde $d$ é o valor do dígito hexadecimal. Para a aritmética, implementamos algoritmos de base-16 para transportes e empréstimos. Esses métodos são verificados conforme os padrões da ciência da computação para assegurar que tarefas de aritmética hexadecimal sejam executadas com precisão absoluta.

🔢Experimente Mais Calculadoras

Calculadora de Porcentagem
Calculadora de Frações
Calculadora de Inclinação
Nota: Esta calculadora foi projetada para fornecer estimativas úteis para fins informativos. Embora nos esforcemos pela precisão, os resultados podem variar com base nas leis locais e circunstâncias individuais. Recomendamos consultar um consultor profissional para decisões críticas.