Calcolatore Z-Score

Determina la posizione standardizzata di qualsiasi punto dati all’interno di una distribuzione normale.

Z-score: —

Convertitore Z-score ↔ Probabilità

P(x < Z)
—
P(x > Z)
—
P(0 < x < Z)
—
P(-Z < x < Z)
—
P(x < -Z o x > Z)
—

Esempi di calcolo

Caso di calcolo Risultato
Valore 85, Media 70, Deviazione 10 Z-score = 1,5
Significato di uno Z-score negativo Il valore è inferiore alla media
Uso in test standardizzati (es. test d’ingresso) Posizionamento statistico del risultato

Come usare il Calcolatore Z-Score?

Servono solo tre dati. Inserisci il punteggio grezzo osservato (il punto dati che stai analizzando). Poi indica la media della popolazione – la media aritmetica dell’intera distribuzione di riferimento. Infine, inserisci la deviazione standard della popolazione – la misura di dispersione di quella stessa popolazione. Una volta completati i tre campi e premuto “Calcola”, il risultato appare immediatamente come z-score, indicando di quante deviazioni standard il valore è sopra (positivo) o sotto (negativo) la media.

Come viene calcolato lo Z-Score

Lo z-score – detto anche punteggio standard – si ottiene sottraendo la media della popolazione al punteggio grezzo e dividendo la differenza per la deviazione standard della popolazione. Il valore risultante posiziona l’osservazione originale sulla distribuzione normale standard (media = 0, deviazione standard = 1), semplificando i calcoli di probabilità e i confronti statistici.Tabella Z

Suggerimenti utili 💡

  • Usa i parametri della popolazione quando sono noti; per dati campionari valuta il t-score invece dello z-score
  • Valori con |z| > 3 sono generalmente considerati insoliti o potenziali outlier in dati normalmente distribuiti

📋Passaggi per Calcolare

  1. Inserisci il punteggio grezzo osservato

  2. Inserisci la media della popolazione (μ)

  3. Inserisci la deviazione standard della popolazione (σ)

Errori comuni ⚠️

  1. Utilizzare la deviazione standard del campione invece di quella della popolazione.
  2. Dimenticare di sottrarre la media dal valore prima di dividere per la deviazione standard.
  3. Pensare che un valore di Z-score superiore a 3 sia impossibile (è raro, ma possibile).
  4. Confondere il valore dello Z-score con il valore di probabilità (p-value) delle tavole.

Applicazioni pratiche📊

  1. Standardizzare i punteggi dei test (SAT, GRE, QI) per confronti equi tra versioni diverse

  2. Rilevare outlier in dataset di ricerca e controllo qualità

  3. Calcolare probabilità e percentili in variabili a distribuzione normale

Domande Frequenti

Cos’è uno z-score in statistica?

Uno z-score rappresenta la distanza di un punteggio grezzo dalla media della popolazione espressa in unità di deviazione standard della popolazione. Trasforma qualsiasi distribuzione normale nella distribuzione normale standard, permettendo l’uso di tabelle standardizzate e calcoli di probabilità.

Come calcolare manualmente uno z-score?

Sottrai la media della popolazione al valore osservato e dividi il risultato per la deviazione standard della popolazione. La formula universale è z = (x − μ) / σ quando i parametri della popolazione sono noti. I calcolatori online eseguono l’operazione istantaneamente ed eliminano errori di calcolo.

Come trovare lo z-score quando media e deviazione standard sono note?

Con il punteggio grezzo (x), la media della popolazione (μ) e la deviazione standard della popolazione (σ) basta sostituire direttamente nella formula dello z-score per ottenere il valore standardizzato. È l’approccio standard in statistica inferenziale e nei test di ipotesi.

Cosa indica uno z-score negativo?

Un punteggio standard negativo indica che il punto dati si trova sotto la media della popolazione. Ad esempio, uno z-score di −1.5 significa che il valore è 1.5 deviazioni standard sotto la media della distribuzione.

Come si usa lo z-score per trovare probabilità?

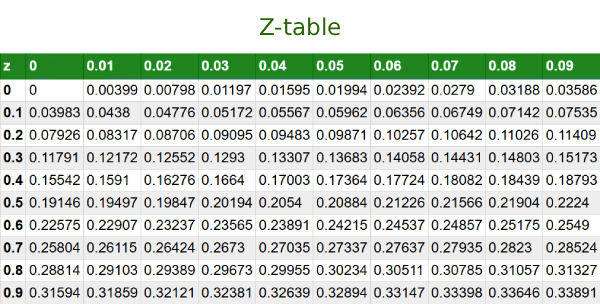
Dopo aver ottenuto lo z-score, consulta la tabella della distribuzione normale standard (tabella Z) o la funzione di distribuzione cumulativa per determinare l’area sotto la curva. Quest’area corrisponde alla probabilità di osservare un valore minore o uguale al punteggio standardizzato.

Quale formula usa questo calcolatore di z-score?

Il calcolatore applica la formula standard riconosciuta in tutto il mondo: z = (x − μ) / σ, dove x è il punteggio grezzo, μ la media della popolazione e σ la deviazione standard della popolazione. Formalizzata all’inizio del XX secolo e avallata dalla Royal Statistical Society e dall’American Statistical Association, rimane il pilastro della standardizzazione nell’analisi della distribuzione normale.

Come interpretare i risultati dello z-score?

Uno z-score pari a 0 posiziona l’osservazione esattamente alla media della popolazione. Circa il 68% dei dati cade entro ±1, il 95% entro ±2 e il 99.7% entro ±3 deviazioni standard in una distribuzione normale. Valori assoluti maggiori indicano osservazioni sempre più rare rispetto alla popolazione data.

🔢Prova Altri Calcolatori

Calcolatore del Resto
Calcolatrice Esadecimale
Calcolatore Deviazione Standard
Nota: Questo calcolatore è progettato per fornire stime utili a scopo informativo. Sebbene ci sforziamo di garantire l'accuratezza, i risultati possono variare in base alle leggi locali e alle circostanze individuali. Si consiglia di consultare un consulente professionale per decisioni importanti.