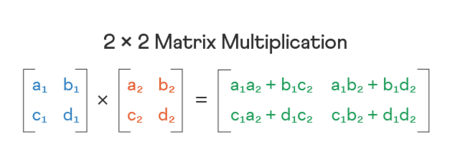Calculadora de Matrices

Calculadora de Matrices para Operaciones, Determinantes e Inversas.

Por favor, ingrese los detalles requeridos y haga clic en Calcular.

¿Te ha resultado útil esta calculadora?

★ ★ ★ ★ ★
4.8/5 (17 votos)

Ejemplos de cálculo

Caso de cálculo Resultado
Determinante de matriz 2x2 ad - bc
Multiplicación A × B Nueva matriz C
Matriz identidad Diagonal de 1s

¿Cómo Usar la Calculadora de Matrices?

Para utilizar la Calculadora de Matrices, primero selecciona la operación que deseas realizar, como la suma, resta, multiplicación, cálculo del determinante o la matriz inversa. Define las dimensiones de tus matrices (filas y columnas). Es fundamental recordar que para la multiplicación de matrices, el número de columnas de la primera matriz debe coincidir exactamente con el número de filas de la segunda. Una vez establecidas las dimensiones, introduce los valores numéricos en cada celda y haz clic en "Calcular". La herramienta procesará los datos y te mostrará el resultado final, junto con una explicación paso a paso en operaciones complejas para facilitar tu aprendizaje.

¿Cómo se Realizan los Cálculos de Matrices?

La forma en que se realiza cada operación depende directamente de cada operación única. La suma y la resta también se realizan elemento por elemento, pero requieren matrices de las mismas dimensiones. Para los determinantes de matrices de 2x2 y 3x3 se aplica la fórmula estándar, mientras que para matrices más grandes se utiliza el método de reducción por filas.

La inversa se calcula mediante eliminación gaussiana o métodos de adjuntos, proporcionando un resultado aplicando estas fórmulas cuando sea necesario.

Diagrama de Multiplicación de Matrices 2x2

Guía de Uso y Consejos 💡

  • Verifica que las dimensiones sean compatibles antes de intentar una multiplicación.
  • Si el determinante es 0, recuerda que la matriz no tiene inversa.

📋Pasos para Calcular

  1. Selecciona la operación matemática (Suma, Multiplicación, Determinante, etc.).

  2. Configura el tamaño de la matriz (número de filas y columnas).

  3. Ingresa los números en las celdas y pulsa "Calcular".

Errores a evitar ⚠️

  1. Intentar multiplicar matrices cuyas dimensiones no son compatibles.
  2. No respetar el orden de la multiplicación (A x B no es igual a B x A).
  3. Cometer errores de signos al calcular el determinante o la matriz inversa.
  4. Confundir las filas (horizontales) con las columnas (verticales) al ingresar datos.

Aplicaciones Prácticas📊

  1. Resolver ecuaciones lineales en álgebra usando operaciones de matrices.

  2. Analizar transformaciones de datos en gráficos por computadora.

  3. Optimizar sistemas de ingeniería con cálculos de matrices.

Preguntas Frecuentes (FAQ)

¿Qué es una calculadora de matrices?

Es un motor de computación lineal que procesa arreglos rectangulares de números ($$m \times n$$). Permite ejecutar operaciones complejas como el cálculo de determinantes, la transposición, la inversión y la multiplicación escalar o matricial. Es una herramienta fundamental en física, estadística, computación gráfica y resolución de sistemas de ecuaciones lineales.

¿Cómo multiplicar matrices?

La multiplicación no es conmutativa ($$A \cdot B \neq B \cdot A$$). Para obtener el elemento $$c_{ij}$$ del producto, se realiza el producto escalar de la fila $$i$$ de la primera matriz por la columna $$j$$ de la segunda: $$c_{ij} = \sum_{k=1}^{n} a_{ik}b_{kj}$$. El número de columnas de la primera debe coincidir con el de filas de la segunda.

¿Qué es el determinante?

Es una función escalar que asigna un número único a una matriz cuadrada. Se denota como $$\det(A)$$ o $$|A|$$. Es un indicador crítico: si el determinante es cero, la matriz es "singular" y no tiene inversa, lo que significa que el sistema de ecuaciones asociado no tiene una solución única.

¿Para qué sirve la inversa?

La matriz inversa ($$A^{-1}$$) es aquella que, multiplicada por la original, da como resultado la matriz identidad ($$I$$). Matemáticamente: $$A \cdot A^{-1} = I$$. Se utiliza para resolver ecuaciones matriciales de la forma $$AX = B$$, donde $$X = A^{-1}B$$, esencial en el modelado de redes y circuitos.

¿Cómo se usa en la ingeniería estructural en España?

En España, el cumplimiento del Código Técnico de la Edificación (CTE) requiere el análisis de estructuras mediante el método de rigidez matricial. Los ingenieros utilizan matrices para calcular desplazamientos y tensiones en estructuras complejas, modelando cada nodo como una variable en un sistema matricial masivo.

¿Qué fórmulas se usan en la calculadora de matrices?

Aplicamos el método de eliminación de Gauss-Jordan para inversiones y la Regla de Sarrus o el desarrollo por cofactores (Teorema de Laplace) para determinantes: $$\det(A) = \sum_{j=1}^{n} (-1)^{i+j} a_{ij} M_{ij}$$. Estas técnicas aseguran precisión incluso en matrices de gran dimensión.

¿Qué es la transpuesta de una matriz?

Es la operación de intercambiar filas por columnas. Si una matriz $$A$$ tiene dimensiones $$m \times n$$, su transpuesta $$A^T$$ tendrá dimensiones $$n \times m$$. Es una operación básica pero vital en el cálculo de regresiones lineales y econometría.

🔢Otras herramientas que podrían interesarte

Calculadora de Trigonometría
Calculadora de Logaritmos
Calculadora de Círculo
Nota: Esta calculadora está diseñada para ofrecer estimaciones útiles con fines informativos. Aunque nos esforzamos por la precisión, los resultados pueden variar según las leyes locales y las circunstancias individuales. Recomendamos consultar con un asesor profesional para decisiones importantes.