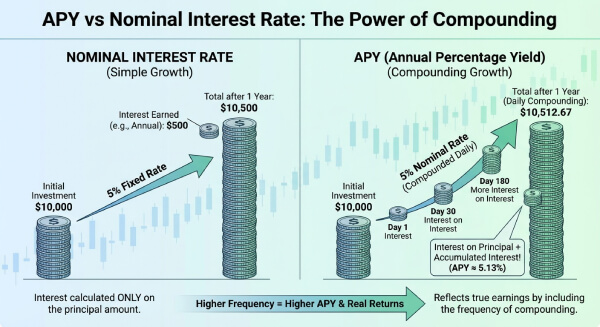
APY-Rechner
Ermitteln Sie die tatsächliche effektive Jahresrendite Ihrer Ersparnisse oder Investitionen, indem Sie die Kraft des Zinseszinses berücksichtigen.
Berechnungsbeispiele
Wie berechnet man die jährliche Rendite (APY)?
Der APY-Rechner (Annual Percentage Yield) ist ein unverzichtbares Werkzeug zum Vergleich von Finanzprodukten wie Tagesgeldkonten, Festgeldern und Geldmarktfonds. Um eine genaue Berechnung zu erhalten, müssen Sie folgende Daten angeben:
1. Nominaler Zinssatz: Dies ist der von der Bank angegebene jährliche Sollzins (APR).
2. Zinsintervall (Zinskapitalisierung): Dies bestimmt, wie oft Zinsen berechnet und Ihrem Guthaben gutgeschrieben werden (z. B. täglich, monatlich oder vierteljährlich).
Wenn Sie auf "Berechnen" klicken, ermittelt das Tool den effektiven Jahreszins. Im Gegensatz zum einfachen Zinssatz berücksichtigt der APY den "Zinseszins-Effekt". Wenn Sie beispielsweise ein Hochzins-Sparkonto haben, führt eine häufigere Verzinsung zu einem höheren APY, selbst wenn der Nominalzins gleich bleibt. Dieses Tool hilft Sparern, die profitabelsten Optionen bei verschiedenen Banken zu identifizieren.
Die Mathematik hinter dem Zinseszins
Der Unterschied zwischen dem nominalen Zinssatz und dem APY liegt im Zinseszinseffekt. Während der Nominalzins der periodische Zinssatz multipliziert mit der Anzahl der Perioden im Jahr ist, spiegelt der APY das tatsächliche Wachstum über 365 Tage wider.
Die standardmäßige APY-Formel, die unser Rechner verwendet, lautet:
$$APY = \left( 1 + \frac{r}{n} \right)^n - 1$$
Wobei:
- r der nominale jährliche Zinssatz ist (als Dezimalzahl).
- n die Anzahl der Zinsperioden pro Jahr ist.
Mit diesem Finanzanalyse-Tool können Sie sehen, wie eine tägliche Verzinsung ($n=365$) die jährliche Verzinsung ($n=1$) übertrifft. Unser Rechner stellt sicher, dass Ihre Prognosen für die Altersvorsorge oder den Notgroschen mathematisch präzise sind.
Nützliche Tipps 💡
- Achten Sie bei der Eröffnung eines Kontos immer auf den APY (Effektivzins) statt nur auf den Nominalzins, da dieser Ihren tatsächlichen Gewinn darstellt.
- Kleine Unterschiede im APY (z. B. 0,10%) können über einen Zeitraum von 20 Jahren einen Unterschied von mehreren tausend Euro ausmachen.
- Prüfen Sie, ob Ihre Bank ein 360-Tage- oder 365-Tage-Jahr für die tägliche Verzinsung verwendet.
📋Schritte zur Berechnung
-
Geben Sie den nominalen Jahreszinssatz in Prozent ein.
-
Wählen Sie das Zinsintervall (z. B. täglich, monatlich, jährlich).
-
Optional: Geben Sie das Startkapital ein, um den genauen Euro-Betrag zu sehen.
-
Klicken Sie auf Berechnen, um den APY und die Gesamtzinsen anzuzeigen.
Häufige Fehler ⚠️
- Verwechslung von APY und APR: APY gilt für Einlagen (Gewinne), APR wird meist für Kredite (Kosten) verwendet.
- Steuern ignorieren: Der APY zeigt das Bruttowachstum, aber die <b>Abgeltungsteuer</b> kann Ihren Nettoprofit mindern.
- Unterschiedliche Zeiträume: Den Ertrag eines 6-monatigen Festgelds direkt mit dem APY eines Tagesgeldkontos vergleichen.
- Falsche Zinsperiode: Annahme einer jährlichen Verzinsung, obwohl die Bank die Zinsen quartalsweise gutschreibt.
Warum der APY für Ihr Portfolio wichtig ist📊
Bankangebote vergleichen: Nutzen Sie den APY, um ein Tagesgeld mit 3,5% Zinsen (täglich verzinst) gegen ein Festgeld mit 3,55% (jährlich verzinst) zu prüfen.
Investitionsprognosen: Schätzen Sie den zukünftigen Wert von Aktien mit Dividendenreinvestition oder Krypto-Staking-Erträgen.
Inflationsanalyse: Bestimmen Sie, ob Ihr Zinssatz hoch genug ist, um die Kaufkraft nach Steuern zu erhalten.
Zinstreppen: Berechnen Sie die effektive Rendite verschiedener Laufzeiten bei einer Festgeld-Strategie.
Fragen und Antworten
Was ist der APY und wie funktioniert er?
Wie berechne ich den APY aus dem Nominalzins?
$$APY = \left( 1 + \frac{r}{n} \right)^n - 1$$
Beispiel: Bei 5% ($0,05$) monatlicher Verzinsung ($n=12$):
$$APY = \left( 1 + \frac{0,05}{12} \right)^{12} - 1 \approx 0,05116 \text{ oder } 5,116\%$$
Was ist der Unterschied zwischen APR und APY?
Wie beeinflusst die Häufigkeit der Verzinsung den APY?
1. Jährlich: $$n = 1$$
2. Vierteljährlich: $$n = 4$$
3. Monatlich: $$n = 12$$
4. Täglich: $$n = 365$$
Eine tägliche Verzinsung liefert in der Regel die höchste Rendite für einen festen Nominalzinssatz.
Ist der APY dasselbe wie die Gesamtrendite (ROI)?
Welche Formel nutzt dieser APY-Rechner genau?
$$APY = 100 \times \left[ \left( 1 + \frac{\text{Zinsen}}{\text{Kapital}} \right)^{365/\text{Laufzeit}} - 1 \right]$$
Dies bietet 100%ige Genauigkeit für Finanzplanungen und Bankvergleiche.