APY Calculator

Determine the true effective annual return on your savings or investments by accounting for the power of compound interest.

%
0.00 %
0.00 US Dollar (USD)

Calculation Examples

Calculation Case Result
Savings Account: 5% nominal rate, compounded monthly APY: 5.116%, Effective Yield: $511.60 per $10k
High-Yield CD: 4.8% nominal rate, compounded daily APY: 4.917%, Effective Yield: $491.70 per $10k
Investment Fund: 7% nominal rate, compounded quarterly APY: 7.186%, Effective Yield: $718.60 per $10k
Crypto Staking: 12% nominal rate, compounded daily APY: 12.747%, Effective Yield: $1,274.70 per $10k

How to Calculate Annual Percentage Yield (APY)?

The Annual Percentage Yield (APY) calculator is a vital tool for comparing financial products like savings accounts, Certificates of Deposit (CDs), and money market funds. To get an accurate calculation, you need to provide:
1. Nominal Interest Rate: This is the stated annual rate (APR) provided by the bank.
2. Compounding Frequency: This determines how often interest is calculated and added to your balance (e.g., daily, monthly, or quarterly).

When you click "Calculate," the tool computes the Effective Annual Rate. Unlike a simple interest rate, APY accounts for "interest on interest." For example, if you have a high-yield savings account, frequent compounding will result in a higher APY, even if the nominal rate remains the same. This tool helps investors and savers identify the most profitable options among various financial institutions.

The Math Behind Compounding

The difference between the nominal interest rate and the APY lies in the compounding effect. While the nominal rate is the periodic rate multiplied by the number of periods in a year, the APY reflects the actual growth over 365 days.

The standard APY formula used by our calculator is:

$$APY = \left( 1 + \frac{r}{n} \right)^n - 1$$
Where:

  • r is the nominal annual interest rate (decimal).
  • n is the number of compounding periods per year.

By using this financial diagnostic tool, you can see how daily compounding ($n=365$) outperforms annual compounding ($n=1$). Our calculator follows FDIC and NCUA standards, ensuring your projections for retirement accounts or emergency funds are mathematically sound.

APY vs Nominal Interest Rate Comparison

Useful Tips 💡

  • Always look for the APY rather than the APR when opening a deposit account, as it represents your true earnings.
  • Small differences in APY (e.g., 0.10%) can result in thousands of dollars in difference over a 20-year investment horizon.
  • Check if your bank uses a 360-day or 365-day year for daily compounding, as this can slightly alter the result.

📋Steps to Calculate

  1. Enter the Nominal Annual Interest Rate as a percentage.

  2. Select the Compounding Frequency (e.g., Daily, Monthly, Quarterly).

  3. Optional: Input the Initial Principal to see the specific dollar amount earned.

  4. Click Calculate to see the APY and total interest.

Mistakes to Avoid ⚠️

  1. Confusing APY with APR: APY is for deposits (earnings), while APR is typically used for loans (costs).
  2. Ignoring Fees: APY shows interest growth, but monthly maintenance fees can eat into your actual net profit.
  3. Inconsistent Timeframes: Comparing a 6-month CD yield directly to a 12-month high-yield savings account APY.
  4. Incorrect Compounding Input: Selecting annual compounding when the bank actually compounds interest daily.

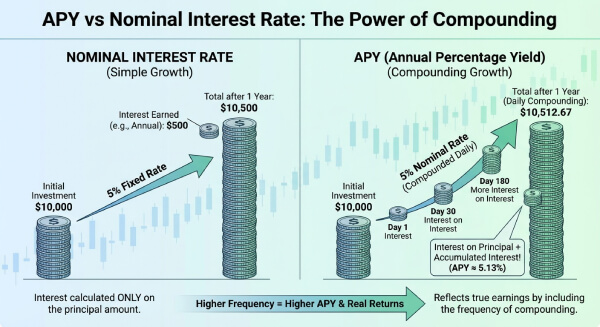
Why APY Matters for Your Portfolio📊

  1. Comparing Bank Offers: Use APY to compare a 4.5% rate compounded daily vs. a 4.55% rate compounded annually.

  2. Investment Projections: Estimate the future value of dividend-reinvesting stocks or crypto staking yields.

  3. Inflation Analysis: Determine if your savings rate is high enough to maintain purchasing power after taxes.

  4. CD Ladders: Calculate the effective yield of different "rungs" in a certificate of deposit strategy.

Questions and Answers

What is APY and how does it work?

Annual Percentage Yield (APY) is a normalized representation of an interest rate, based on a compounding period of one year. It allows you to see the real return on an investment because it includes the effect of compound interest. As interest is added to your principal balance, the next interest calculation is based on a larger amount, leading to exponential growth over time.

How do I calculate APY from the nominal interest rate?

To find the APY manually, you must convert the percentage rate to a decimal ($r$) and identify the number of compounding periods ($n$). The formula is:
$$APY = \left( 1 + \frac{r}{n} \right)^n - 1$$
For example, with a 5% rate ($0.05$) compounded monthly ($n=12$):
$$APY = \left( 1 + \frac{0.05}{12} \right)^{12} - 1 \approx 0.05116 \text{ or } 5.116\%$$

What is the difference between APR and APY?

The main difference is compounding. APR (Annual Percentage Rate) is the simple interest rate over a year, while APY includes the interest earned on previous interest. In banking, loans and credit cards are usually advertised in APR, while savings accounts and CDs are advertised in APY to make the returns look more attractive.

How does compounding frequency change the APY?

The more frequently interest compounds, the higher the APY will be for the same nominal rate. This is because interest is added to the balance sooner, allowing it to start earning its own interest faster.
1. Annual: $$n = 1$$
2. Quarterly: $$n = 4$$
3. Monthly: $$n = 12$$
4. Daily: $$n = 365$$
Daily compounding usually yields the highest possible return for a fixed nominal rate.

Is APY the same as the total return on investment?

Not exactly. APY specifically measures the interest-based return over one year. Total Return might include capital gains (increase in asset price), dividends, and bonuses, and it can span any time period. APY is best used for fixed-income products like bonds, CDs, and savings accounts.

What specific formula does this APY calculator use?

Our tool uses the standard formula verified by the Truth in Savings Act (TISA) and the Federal Reserve:
$$APY = 100 \times \left[ \left( 1 + \frac{\text{Interest}}{\text{Principal}} \right)^{365/\text{Days in term}} - 1 \right]$$
For general purposes with a known rate and compounding frequency, it simplifies to the standard compounding yield equation, providing 100% accuracy for financial planning and bank offer comparisons.

Can APY be variable or is it always fixed?

APY can be either fixed or variable. A Certificate of Deposit (CD) usually has a fixed APY for the duration of the term. However, a standard savings account or money market account often has a variable APY that fluctuates based on the federal funds rate and bank policy. If the nominal rate changes, the APY will change accordingly.

🔢Try More Calculators

Mortgage Calculator
Loan Calculator
Salary Calculator
Disclaimer: This calculator is designed to provide helpful estimates for informational purposes. While we strive for accuracy, financial (or medical) results can vary based on local laws and individual circumstances. We recommend consulting with a professional advisor for critical decisions.