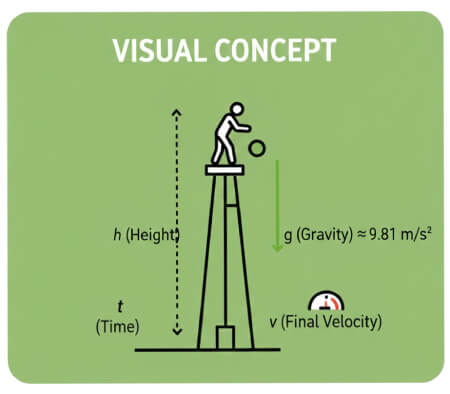
Calcolatore Caduta Libera
Analizza il moto di un oggetto in caduta sotto l'unica influenza della gravità.
Metodo di calcolo (passo per passo)
Assunzioni: velocità iniziale zero, nessuna resistenza dell'aria. Equazioni cinematiche utilizzate:
- h = ½ g t² — altezza / distanza percorsa
- v = g t — velocità finale all'impatto
- t = √(2h / g) — tempo di caduta
- h = v² / (2g) — altezza dalla velocità
- t = v / g — tempo dalla velocità
Accelerazione di gravità: g = 9.81 m/s²
Esempi di calcolo
Come usare il calcolatore di caduta libera?
Seleziona il parametro target: durata della caduta ($t$), velocità di impatto finale ($v$) o spostamento totale ($d$). Inserisci i dati nei campi rispettivi; per una caduta standard da fermo, assicura che la velocità iniziale ($v_0$) sia zero. Scegli il sistema di coordinate preferito—Metrico ($m, s$) o Imperiale ($ft, s$). L'algoritmo applica l'accelerazione di gravità standard ($g \approx 9.81 \text{ m/s}^2$ o $32.2 \text{ ft/s}^2$). Cliccando su "Calcola", il sistema esegue le equazioni cinematiche per fornire risultati istantanei, inclusi i passaggi intermedi per chiarezza pedagogica. Questo strumento è ottimizzato per la meccanica newtoniana dove la resistenza dell'aria è trascurabile.
Quadro Matematico ed Equazioni Cinematiche
La caduta libera è definita come un moto rettilineo con accelerazione costante. Nel vuoto o ignorando l'attrito aerodinamico, il moto è governato dalle seguenti equazioni fondamentali: 1. Spostamento: $d = \frac{1}{2}gt^2$ | 2. Velocità Finale: $v = gt$ | 3. Relazione Velocità-Spostamento: $v = \sqrt{2gd}$. Dove $g$ rappresenta l'intensità del campo gravitatoriolocale. Queste derivazioni assumono che l'oggetto parta da uno stato di quiete ($v_0 = 0$). In mezzi fluidi (come l'aria), gli oggetti raggiungono infine la velocità terminale a causa delle forze di attrito, un fattore non considerato in questo modello newtoniano semplificato.
Suggerimenti utili 💡
- Assicurati che la velocità iniziale sia zero per scenari di pura caduta da fermo.
- Usa unità coerenti in tutti i campi di input per mantenere l'integrità del calcolo.
📋Passaggi per Calcolare
-
Seleziona la variabile nota (altezza, durata o velocità).
-
Specifica il sistema di unità (Metrico o Imperiale).
-
Esegui il calcolo per ottenere dati cinematici completi.
Errori comuni ⚠️
- Ignorare gli effetti della resistenza dell'aria su oggetti con alto rapporto superficie/massa.
- Confondere massa e peso; nel vuoto, tutti gli oggetti cadono alla stessa velocità indipendentemente dalla massa.
- Misurazioni temporali imprecise in esperimenti manuali che portano a errori esponenziali nella distanza.
- Applicare queste equazioni a velocità relativistiche o campi gravitazionali non uniformi.
Applicazioni Pratiche📊
Calcolo dell'energia di impatto e della velocità per valutazioni di sicurezza strutturale.
Verifica dei dati sperimentali nelle sessioni di laboratorio di meccanica classica.
Stima dell'altezza di strutture verticali basata su cadute temporizzate.
Modellazione della traiettoria iniziale per il rilascio di carichi o fisica dei droni.