Rechner für den freien Fall

Analysieren Sie die Bewegung eines Objekts, das ausschließlich unter dem Einfluss der Schwerkraft fällt. Berechnen Sie Geschwindigkeit, Zeit und Distanz präzise.

Höhe / Gefallene Strecke (m): Fallzeit (s): Endgeschwindigkeit (m/s): Erdbeschleunigung g (m/s²):

Berechnungsmethode (Schritt für Schritt)

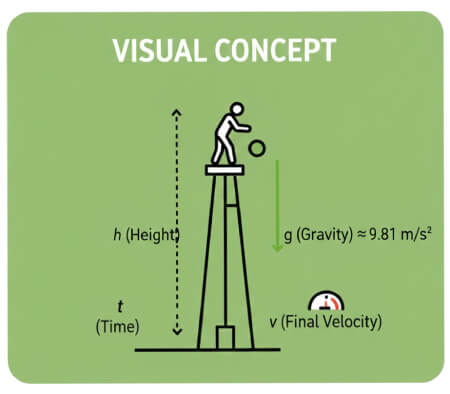
Annahmen: Anfangsgeschwindigkeit null, kein Luftwiderstand. Verwendete kinematische Gleichungen:

h = ½ g t² — Höhe / gefallene Strecke
v = g t — Endgeschwindigkeit beim Aufprall
t = √(2h / g) — Fallzeit
h = v² / (2g) — Höhe aus Geschwindigkeit
t = v / g — Zeit aus Geschwindigkeit

Erdbeschleunigung: g = 9.81 m/s²

Geben Sie genau einen der Werte ein: Höhe, Zeit oder Geschwindigkeit. Der g-Wert kann oben angepasst werden.

Berechnungsbeispiele

Berechnungsfall	Ergebnis
Objekt vom Berliner Fernsehturm gefallen ($368 \text{ m}$)	$t \approx 8,66 \text{ s}, v \approx 84,95 \text{ m/s}$
Fallhöhe von $250 \text{ Fuß}$ (Imperiale Einheiten, $g = 32,2 \text{ ft/s}^2$)	$t \approx 3,94 \text{ s}, v \approx 126,87 \text{ ft/s}$
Falldauer von $5 \text{ Sekunden}$ aus der Ruhe	$d \approx 122,63 \text{ m}, v \approx 49,05 \text{ m/s}$

Wie benutzt man den Freifallrechner?

Um den Freifall-Rechner zu nutzen, definieren Sie Ihre bekannten kinematischen Variablen. Wählen Sie den Zielparameter: Falldauer ($t$), Endgeschwindigkeit ($v$) oder Gesamtdistanz ($d$). Geben Sie die Daten in die entsprechenden Felder ein; für einen Standardfall aus der Ruhe stellen Sie sicher, dass die Anfangsgeschwindigkeit ($v_0$) Null ist. Wählen Sie Ihr bevorzugtes Einheitensystem — Metrisch ($m, s$) oder Imperial ($ft, s$). Der Algorithmus wendet die Standardfallbeschleunigung ($g \approx 9,81 \text{ m/s}^2$ oder $32,2 \text{ ft/s}^2$) an. Nach dem Klicken auf "Berechnen" führt das System die kinematischen Gleichungen aus und liefert sofortige Ergebnisse, einschließlich Zwischenschritten zur pädagogischen Verdeutlichung. Dieses Werkzeug ist für die Newtonsche Mechanik optimiert, bei der der Luftwiderstand als vernachlässigbar gilt.

Mathematischer Rahmen & Kinematische Gleichungen

Der freie Fall ist definiert als eine geradlinige Bewegung mit konstanter Beschleunigung. Im Vakuum oder bei Vernachlässigung des aerodynamischen Widerstands wird die Bewegung durch die folgenden Grundgleichungen bestimmt: 1. Strecke: $d = \frac{1}{2}gt^2$ | 2. Endgeschwindigkeit: $v = gt$ | 3. Geschwindigkeit-Weg-Beziehung: $v = \sqrt{2gd}$. Dabei steht $g$ für die lokale Gravitationsfeldstärke. Diese Ableitungen setzen voraus, dass das Objekt aus dem Ruhezustand ($v_0 = 0$) startet. In fluiden Medien (wie Luft) erreichen Objekte aufgrund von Widerstandskräften schließlich eine Endgeschwindigkeit (Terminalgeschwindigkeit), ein Faktor, der in diesem vereinfachten Newtonschen Modell nicht berücksichtigt wird. Dynamik des freien Falls

Nützliche Tipps 💡

Stellen Sie sicher, dass die Anfangsgeschwindigkeit für einen reinen Fall aus der Ruhe auf Null gesetzt ist.
Verwenden Sie konsistente Einheiten in allen Eingabefeldern, um Berechnungsfehler zu vermeiden.

📋Schritte zur Berechnung

Wählen Sie die bekannte Variable (Höhe, Dauer oder Geschwindigkeit).
Legen Sie das Einheitensystem fest (Metrisch oder Imperial).
Klicken Sie auf "Berechnen", um die vollständigen kinematischen Daten zu erhalten.

Häufige Fehler ⚠️

Ignorieren des Luftwiderstands bei Objekten mit großem Verhältnis von Oberfläche zu Masse.
Verwechslung von Masse und Gewicht; im Vakuum fallen alle Objekte unabhängig von ihrer Masse gleich schnell.
Ungenaue Zeitmessungen bei manuellen Experimenten, die zu exponentiellen Fehlern bei der Distanz führen.
Anwendung dieser Gleichungen auf relativistische Geschwindigkeiten oder ungleichmäßige Gravitationsfelder.

Praktische Anwendungen📊

Berechnung von Aufprallenergie und Geschwindigkeit für bauliche Sicherheitsbewertungen.
Verifizierung experimenteller Daten in Laborsitzungen zur klassischen Mechanik.
Schätzung der Höhe vertikaler Strukturen basierend auf zeitgesteuerten Abwürfen.
Anfängliche Flugbahnmoldellierung für Drohnenphysik und Nutzlastabwürfe.

Fragen und Antworten

Was ist die Definition des freien Falls?

In der Newtonschen Physik ist der freie Fall jede Bewegung eines Körpers, bei der die Schwerkraft die einzige wirkende Kraft ist. Dies setzt eine Vakuumumgebung ohne Luftwiderstand voraus. Unter diesen Bedingungen erfährt das Objekt eine konstante Beschleunigung von $g \approx 9,81 \text{ m/s}^2$ in Richtung Erdmittelpunkt, unabhängig von Masse oder Form.

Wie berechnet man die Fallzeit aus einer bestimmten Höhe?

Um die Falldauer aus einer bekannten Distanz ($d$) abzuleiten, stellen wir die Gleichung $d = \frac{1}{2}gt^2$ um. Das Auflösen nach $t$ ergibt die Formel $t = \sqrt{2d/g}$. Diese Berechnung setzt voraus, dass das Objekt mit einer Anfangsgeschwindigkeit von Null startet.

Wie lautet die Formel für die Endgeschwindigkeit?

Die Geschwindigkeit kurz vor dem Aufprall wird durch die Zeit oder die Distanz bestimmt. Wenn die Zeit bekannt ist, verwenden wir $v = gt$. Wenn die Distanz bekannt ist, nutzen wir die Torricelli-Gleichung: $v = \sqrt{2gd}$.

Berücksichtigt dieses Tool den Luftwiderstand?

Nein, dieser Rechner ist für den "idealen" freien Fall im Vakuum konzipiert. In der Realität nimmt der Luftwiderstand zu, bis er der Gravitationskraft entspricht, woraufhin das Objekt eine konstante Terminalgeschwindigkeit erreicht.

Wird die Masse des Objekts für die Berechnung benötigt?

Nein. Nach dem Äquivalenzprinzip beeinflusst die Masse die Fallrate im Vakuum nicht. Gravitative und träge Masse heben sich in der Bewegungsgleichung ($ma = mg$) auf. Daher benötigt unser Rechner keine Massenangabe.

Welche Konstante wird für die Gravitation verwendet?

Der Rechner verwendet die von der CGPM definierte Standardbeschleunigung $g_n = 9,80665 \text{ m/s}^2$ für metrische Berechnungen und ca. $32,174 \text{ ft/s}^2$ für das imperiale System.

Hinweis: Dieser Rechner dient dazu, hilfreiche Schätzungen zu Informationszwecken bereitzustellen. Obwohl wir uns um Genauigkeit bemühen, können die Ergebnisse je nach örtlichen Gesetzen und individuellen Umständen variieren. Wir empfehlen, bei wichtigen Entscheidungen einen professionellen Berater zu Rate zu ziehen.