Rechner für potentielle Energie

Berechnen Sie die Lageenergie (potentielle Energie) eines Körpers basierend auf Masse, Höhe und lokaler Erdbeschleunigung.

Berechnungsbeispiele

Berechnungsfall Ergebnis
Wanderer (80 kg) auf einer 100 m hohen Alm E_p = 78480 J
Dachziegel (2 kg) in 5 m Höhe auf der Erde E_p = 98.1 J
Mondgestein (10 kg) in 2 m Höhe auf dem Mond ($1.62 \, \text{m/s}^2$) E_p = 32.4 J

Wie verwendet man den Rechner für potentielle Energie?

Unser Rechner für Lageenergie ist ein präzises Werkzeug für Schüler, Studenten und Ingenieure. Geben Sie zunächst die Masse des Objekts in Kilogramm (kg) ein. Wählen Sie dann die Höhe in Metern (m) relativ zu Ihrem Bezugspunkt (meist dem Boden oder einem definierten Nullniveau). Das Tool nutzt standardmäßig die Erdbeschleunigung von $g = 9.81 \, \text{m/s}^2$, erlaubt aber auch Anpassungen für andere Himmelskörper wie den Mond ($1.62 \, \text{m/s}^2$). Das Verständnis der Lageenergie ist essenziell für die Analyse mechanischer Systeme und den Energieerhaltungssatz. Durch die Verwendung konsistenter SI-Einheiten stellen Sie sicher, dass das Ergebnis korrekt in Joule ($J$) ausgegeben wird. Dieses Tool hilft Ihnen bei der Verifizierung von Hausaufgaben oder der Planung technischer Prototypen.

Die mgh-Formel verstehen

Die Berechnung der potentiellen Energie ist ein Grundpfeiler der klassischen Mechanik. Die Energie, die ein Körper aufgrund seiner Position in einem Gravitationsfeld besitzt, wird durch die Formel $E_p = m \cdot g \cdot h$ definiert. In dieser Gleichung steht $m$ für die Masse, $g$ für die Fallbeschleunigung und $h$ für die vertikale Höhe. Diese Beziehung verdeutlicht, dass die Energie direkt proportional zu allen drei Variablen ist: Eine Verdopplung der Höhe führt exakt zu einer Verdopplung der Energie. Diese Formel setzt ein konstantes Gravitationsfeld voraus, was in Erdnähe eine präzise Annäherung ist. Die Einheit Joule ($1 \, J = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$) beschreibt dabei die Arbeit, die verrichtet werden muss, um den Körper gegen die Schwerkraft auf diese Höhe zu heben.Diagramm der potentiellen Energie mgh

Nützliche Tipps 💡

  • Legen Sie vor der Messung ein klares Bezugsniveau fest, um konsistente Ergebnisse zu erhalten.
  • Beachten Sie bei hochpräzisen Berechnungen die Breitengrad-Abhängigkeit der Schwerkraft.
  • Denken Sie daran, dass Energie eine skalare Größe ist und keine Richtung besitzt.

📋Schritte zur Berechnung

  1. Geben Sie die Masse des Objekts in Kilogramm (kg) ein.

  2. Tragen Sie die vertikale Höhe in Metern (m) ein.

  3. Geben Sie die Fallbeschleunigung an (Standard ist $9.81 \, \text{m/s}^2$).

  4. Prüfen Sie das Ergebnis in Joule (J).

Häufige Fehler ⚠️

  1. Verwendung des Gewichts anstelle der Masse; denken Sie daran, dass das Gewicht die Masse multipliziert mit der Fallbeschleunigung ist, nicht nur die Masse selbst.
  2. Mischen von metrischen und imperialen Einheiten, zum Beispiel die Verwendung von Fuß für die Höhe, während 9,81 m/s² für die Erdbeschleunigung angewendet wird.
  3. Ignorieren der Wahl des Bezugsniveaus für die Höhe, was zu fehlerhaften Berechnungen der Änderung der potenziellen Energie führt.
  4. Anwendung der Formel auf astronomische Entfernungen, bei denen die Schwerkraft dem Abstandsgesetz folgt, anstatt konstant zu sein.

Praktische Anwendungen der Lageenergie📊

  1. Berechnung der gespeicherten Energie in Stauseen von Alpen-Wasserkraftwerken.

  2. Analyse der Sicherheit und Mechanik von Achterbahnen und Aufzugssystemen.

  3. Ermittlung der Aufprallenergie fallender Objekte im Arbeitsschutz und Bauwesen.

  4. Lösung komplexer Physikaufgaben zur mechanischen Energieerhaltung ($E_{ges} = E_p + E_{kin}$).

Fragen und Antworten

Was ist die Formel für potentielle Energie?

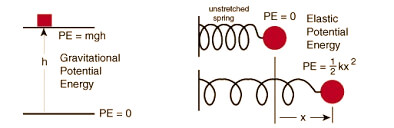
Die physikalische Standardformel zur Berechnung der potentiellen Energie (Lageenergie) lautet $E_p = m \cdot g \cdot h$. In dieser Gleichung repräsentiert $m$ die Masse des Objekts in Kilogramm (kg), $g$ ist die Erdbeschleunigung (auf der Erde etwa $9.81 \, \text{m/s}^2$) und $h$ steht für die vertikale Höhe in Metern (m) über einem gewählten Bezugspunkt. Da es sich um eine rein multiplikative Verknüpfung handelt, steigt die Energie linear mit jedem dieser Faktoren an.

Wie berechnet man Joule?

Um die Energie in der SI-Einheit Joule ($J$) zu erhalten, müssen alle Eingangswerte in Standardeinheiten vorliegen. Multiplizieren Sie die Masse in kg mit der Fallbeschleunigung in $\text{m/s}^2$ und der Höhe in Metern. Ein Joule ist definiert als die Energie, die benötigt wird, um eine Kraft von einem Newton über eine Strecke von einem Meter auszuüben: $1 \, J = 1 \, \text{N} \cdot \text{m} = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$. Unser Rechner übernimmt diese Umrechnung automatisch für Sie.

Was ist die Einheit der potentiellen Energie?

Die offizielle SI-Einheit für potentielle Energie ist das Joule ($J$). In der Technik und im Alltag begegnen uns oft auch Kilojoule ($1 \, kJ = 1000 \, J$) oder Megajoule ($MJ$), insbesondere bei der Angabe von Nährwerten oder großen mechanischen Arbeiten. Historisch wurde oft die Kalorie verwendet, doch in der modernen Physik ist das Joule die universelle Einheit für alle Energieformen, einschließlich kinetischer und thermischer Energie.

Ist die Lageenergie vom Pfad abhängig?

Nein, die potentielle Energie in einem konservativen Gravitationsfeld ist streng pfadunabhängig. Das bedeutet, es spielt keine Rolle, ob ein Objekt senkrecht nach oben gehoben oder über eine schräge Rampe an seine Position gebracht wurde. Maßgeblich für die Berechnung ist einzig und allein der vertikale Höhenunterschied ($h$) zwischen dem Startpunkt und dem Endpunkt relativ zum Bezugsniveau.

Kann potentielle Energie negativ sein?

Ja, die potentielle Energie kann negative Werte annehmen, da sie immer relativ zu einem frei gewählten Bezugspunkt definiert ist. Wenn Sie den Boden als Nullniveau ($h = 0$) festlegen, hat ein Objekt in einem 5 Meter tiefen Brunnen eine negative potentielle Energie. Dies signalisiert physikalisch, dass Arbeit aufgewendet werden muss, um das Objekt zurück auf das Nullniveau zu heben.

Wie wirkt sich die Masse aus?

Die potentielle Energie steht in einem direkt proportionalen Verhältnis zur Masse des Körpers. Wenn zwei Objekte auf die gleiche Höhe gehoben werden, besitzt das schwerere Objekt proportional mehr Energie. Beispielsweise hat ein 100 kg schweres Gewicht genau die zehnfache Lageenergie eines 10 kg schweren Gewichts, sofern beide am selben Ort und auf derselben Höhe gemessen werden.

Welche Methode nutzt dieser Rechner?

Dieser Rechner nutzt die klassische Newtonsche mgh-Gleichung: $E_p = m \cdot g \cdot h$. Diese Methode ist der weltweit anerkannte Standard in der Physik-Ausbildung und im Maschinenbau für Szenarien, in denen die Schwerkraft als konstant betrachtet werden kann. Für Berechnungen in extremen Höhen (z. B. Satellitenbahnen) müssten allgemeinere Gravitationsformeln verwendet werden, aber für bodennahe Anwendungen ist unser Rechner absolut präzise.

🔢Weitere Rechner Ausprobieren

Arbeitsrechner (Physik)
Kinetische Energie Rechner
Impulsrechner
Hinweis: Dieser Rechner dient dazu, hilfreiche Schätzungen zu Informationszwecken bereitzustellen. Obwohl wir uns um Genauigkeit bemühen, können die Ergebnisse je nach örtlichen Gesetzen und individuellen Umständen variieren. Wir empfehlen, bei wichtigen Entscheidungen einen professionellen Berater zu Rate zu ziehen.