Calculadora de Energía Potencial

Calcule la energía potencial gravitatoria (GPE) de un objeto en función de su masa, altura y la aceleración de la gravedad local.

Ejemplos de cálculo

Caso de cálculo Resultado
Piedra de 10 kg a 2 m de altura en la Tierra EP = 196.2 J
Balón de 500 g (0.5 kg) a 10 m de altura en la Tierra EP = 49.05 J
Astronauta de 100 kg a 5 m de altura en la Luna ($1.62 \, \text{m/s}^2$) EP = 810 J

¿Cómo usar la calculadora de energía potencial?

Nuestra calculadora de energía potencial gravitatoria está diseñada para ofrecer precisión tanto en entornos académicos como profesionales. Para comenzar, introduzca la masa del objeto en kilogramos (kg). Luego, especifique la altura en metros (m) relativa a su punto de referencia (normalmente el suelo). La herramienta incluye el valor predeterminado de la gravedad terrestre, $g = 9.81 \, \text{m/s}^2$, pero puede ajustarse para cálculos en otros cuerpos celestes como la Luna ($1.62 \, \text{m/s}^2$) o Marte ($3.71 \, \text{m/s}^2$). Comprender la energía potencial es crucial para analizar sistemas mecánicos y las leyes de conservación de la energía. Al usar unidades consistentes del SI, asegura que el resultado se refleje correctamente en Julios ($J$). Esta herramienta es esencial para verificar tareas escolares o diseñar prototipos de ingeniería.

Entendiendo la fórmula de la energía potencial (mgh)

El cálculo de la energía potencial gravitatoria es un pilar de la mecánica clásica. La energía que posee un objeto debido a su posición en un campo gravitatorio se define por la fórmula: $E_p = m \cdot g \cdot h$. En esta ecuación, $m$ representa la masa, $g$ es la aceleración gravitatoria y $h$ es la altura vertical. Esta relación muestra que la energía potencial es directamente proporcional a las tres variables. Por ejemplo, duplicar la altura de un objeto duplicará exactamente su energía potencial. Esta fórmula asume que el campo gravitatorio es constante, una aproximación exacta cerca de la superficie planetaria. La unidad resultante, el Julio ($1 \, J = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$), cuantifica el trabajo necesario para elevar el objeto a esa altura específica.Diagrama de Energía Potencial Gravitatoria mgh

Guía de Uso y Consejos 💡

  • Defina siempre un punto de referencia claro (nivel cero) antes de medir la altura para mantener la consistencia.
  • Para cálculos aeroespaciales de alta precisión, considere las variaciones locales de la gravedad según la latitud.
  • Recuerde que la energía potencial es una magnitud escalar; tiene magnitud pero no dirección.

📋Pasos para Calcular

  1. Ingrese la masa del objeto en kilogramos (kg).

  2. Introduzca la altura vertical en metros (m).

  3. Especifique la aceleración gravitatoria (por defecto $9.81 \, \text{m/s}^2$).

  4. Revise el resultado de la energía potencial en Julios (J).

Errores a evitar ⚠️

  1. Usar el peso en lugar de la masa; recuerda que el peso es la masa multiplicada por la aceleración de la gravedad, no solo la masa en sí misma.
  2. Mezclar unidades métricas e imperiales, por ejemplo, usar pies para la altura mientras se aplica 9,81 m/s² para la aceleración gravitatoria.
  3. Ignorar la elección del nivel de referencia para la altura, lo que conduce a cálculos incorrectos del cambio en la energía potencial.
  4. Aplicar la fórmula a distancias astronómicas donde la gravedad sigue la ley del cuadrado inverso en lugar de ser constante.

Aplicaciones prácticas de la energía potencial📊

  1. Calcular la energía almacenada en los embalses de presas hidroeléctricas antes de su conversión.

  2. Analizar la seguridad y mecánica de montañas rusas y ascensores en parques de atracciones.

  3. Evaluar la fuerza de impacto de objetos que caen en ingeniería de seguridad y construcción.

  4. Resolver problemas de física que involucran la conservación de la energía mecánica ($EM = EP + EC$).

Preguntas Frecuentes (FAQ)

¿Cuál es la fórmula de la energía potencial?

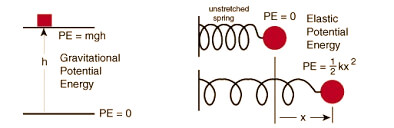
La fórmula estándar de la física para calcular la energía potencial gravitatoria es $E_p = m \cdot g \cdot h$. En esta ecuación, $m$ representa la masa del objeto en kilogramos (kg), $g$ es la aceleración de la gravedad (aproximadamente $9.81 \, \text{m/s}^2$ en la Tierra) y $h$ es la altura vertical en metros (m) sobre un punto de referencia elegido. Al ser una relación multiplicativa, la energía aumenta proporcionalmente con cada una de estas variables.

¿Cómo se calcula la energía potencial en Julios?

Para obtener el resultado en la unidad del SI, el Julio ($J$), debe multiplicar la masa en kg por la gravedad en $\text{m/s}^2$ y la altura en metros. Un Julio se define como el trabajo realizado por una fuerza de un Newton al desplazar un objeto un metro: $1 \, J = 1 \, \text{N} \cdot \text{m}$. Nuestra calculadora realiza este proceso automáticamente para ofrecerle un valor preciso al instante.

¿Cuál es la unidad de la energía potencial?

La unidad oficial del Sistema Internacional para la energía potencial es el Julio ($J$). En contextos técnicos o nutricionales, también es común ver kilojulios ($1 \, kJ = 1000 \, J$) o megajulios ($MJ$). El Julio es una unidad universal que permite comparar la energía potencial con otras formas de energía, como la cinética o la térmica, facilitando el análisis de la conservación de la energía.

¿Depende la energía potencial del camino seguido?

No, la energía potencial gravitatoria es independiente del camino seguido. Esto significa que no importa si un objeto se elevó verticalmente o mediante una rampa inclinada; si la altura final es la misma, la energía potencial será idéntica. Solo depende del desplazamiento vertical neto ($h$) entre el punto inicial y la posición final.

¿Puede la energía potencial ser negativa?

Sí, la energía potencial puede ser negativa porque siempre se mide con respecto a un nivel de referencia arbitrario ($h = 0$). Si define el suelo como nivel cero, un objeto en un sótano o pozo tendrá energía potencial negativa. Esto indica que se requiere realizar un trabajo positivo sobre el objeto para devolverlo al nivel de referencia.

¿Cómo afecta la masa a la energía potencial?

La energía potencial es directamente proporcional a la masa. Si duplica la masa de un cuerpo manteniendo constante la altura y la gravedad, su energía potencial se duplicará exactamente. Por esta razón, los objetos muy pesados a grandes alturas poseen una enorme capacidad de realizar trabajo, como ocurre en las presas hidroeléctricas.

¿Qué fórmula usa esta calculadora?

Esta calculadora aplica rigurosamente la ecuación clásica $E_p = m \cdot g \cdot h$. Este es el estándar global en educación física e ingeniería mecánica para cálculos realizados cerca de la superficie terrestre. Para cálculos a distancias astronómicas, se requeriría la ley de gravitación universal, pero la fórmula mgh es extremadamente precisa para el uso cotidiano y profesional.

🔢Otras herramientas que podrían interesarte

Calculadora de Trabajo
Calculadora de Energía Cinética
Calculadora de Momento
Nota: Esta calculadora está diseñada para ofrecer estimaciones útiles con fines informativos. Aunque nos esforzamos por la precisión, los resultados pueden variar según las leyes locales y las circunstancias individuales. Recomendamos consultar con un asesor profesional para decisiones importantes.