Kalkulator Energi Potensial

Hitung energi potensial gravitasi (GPE) sebuah benda berdasarkan massa, ketinggian, dan percepatan gravitasi lokal.

Contoh Perhitungan

Kasus Perhitungan Hasil
Batu 10 kg, Tinggi 2 m di Bumi PE = 196.2 J
Buah Kelapa 500 g (0.5 kg), Tinggi 10 m di Bumi PE = 49.05 J
Massa 100 kg, Tinggi 5 m di Bulan ($1.62 \, \text{m/s}^2$) PE = 810 J

Bagaimana Cara Menggunakan Kalkulator Energi Potensial?

Kalkulator energi potensial gravitasi kami dirancang untuk presisi dan kemudahan penggunaan baik dalam lingkungan akademik maupun profesional. Untuk memulai, masukkan massa benda dalam satuan kilogram (kg). Selanjutnya, tentukan ketinggian dalam satuan meter (m) relatif terhadap titik acuan Anda — biasanya permukaan tanah atau titik terendah dalam sistem fisik Anda. Alat ini menyertakan nilai default gravitasi Bumi, $g = 9.81 \, \text{m/s}^2$, namun nilai ini dapat disesuaikan untuk perhitungan pada benda langit lain seperti Bulan ($1.62 \, \text{m/s}^2$) atau Mars ($3.71 \, \text{m/s}^2$). Memahami energi potensial sangat penting untuk menganalisis sistem mekanik dan hukum kekekalan energi. Dengan memasukkan unit SI yang konsisten, Anda memastikan output tercermin secara akurat dalam Joule ($J$). Alat ini adalah sumber daya penting untuk memverifikasi tugas sekolah atau merancang prototipe teknik.

Memahami Rumus GPE (mgh)

Perhitungan energi potensial gravitasi adalah landasan mekanika klasik. Energi yang dimiliki suatu benda karena posisinya dalam medan gravitasi didefinisikan oleh rumus: $E_p = m \cdot g \cdot h$. Dalam persamaan ini, $m$ mewakili massa, $g$ adalah percepatan gravitasi, dan $h$ adalah tinggi vertikal. Hubungan ini menunjukkan bahwa energi potensial berbanding lurus dengan ketiga variabel tersebut. Sebagai contoh, menggandakan ketinggian suatu benda akan menggandakan energi potensialnya secara tepat. Rumus khusus ini, yang sering disebut persamaan mgh, mengasumsikan bahwa medan gravitasi konstan, yang merupakan perkiraan yang sangat akurat untuk objek di dekat permukaan planet. Satuan yang dihasilkan, Joule ($1 \, J = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$), mengukur usaha yang diperlukan untuk mengangkat benda ke ketinggian tertentu melawan gaya gravitasi.Diagram Energi Potensial Gravitasi mgh

Tips & Informasi 💡

  • Selalu tentukan titik acuan yang jelas (level nol) sebelum mengukur tinggi untuk memastikan konsistensi.
  • Untuk perhitungan kedirgantaraan presisi tinggi, perhitungkan variasi lokal gravitasi Bumi berdasarkan garis lintang.
  • Ingatlah bahwa energi potensial adalah besaran skalar; ia memiliki nilai tetapi tidak memiliki arah tertentu.

📋Langkah Menghitung

  1. Masukkan massa benda dalam kilogram (kg).

  2. Masukkan tinggi vertikal dalam meter (m).

  3. Tentukan percepatan gravitasi (default $9.81 \, \text{m/s}^2$).

  4. Lihat hasil perhitungan energi potensial dalam Joule (J).

Kesalahan yang Harus Dihindari ⚠️

  1. Menggunakan berat, bukan massa; ingatlah bahwa berat adalah massa dikalikan dengan percepatan gravitasi, bukan hanya massa itu sendiri.
  2. Mencampur satuan metrik dan imperial, misalnya menggunakan kaki untuk tinggi saat menerapkan 9,81 m/s² untuk percepatan gravitasi.
  3. Mengabaikan pemilihan tingkat acuan untuk tinggi, yang menyebabkan kesalahan perhitungan perubahan energi potensial.
  4. Menerapkan rumus pada jarak astronomis di mana gravitasi mengikuti hukum kuadrat terbalik alih-alih konstan.

Aplikasi Praktis Energi Potensial📊

  1. Menghitung energi yang tersimpan dalam waduk bendungan hidroelektrik sebelum diubah menjadi listrik.

  2. Menganalisis keamanan dan mekanika roller coaster serta lift.

  3. Mengevaluasi gaya benturan benda jatuh dalam teknik keselamatan dan konstruksi.

  4. Menyelesaikan masalah fisika kompleks yang melibatkan kekekalan energi mekanik ($EM = EP + EK$).

Pertanyaan Seputar Layanan Kami

Apa rumus energi potensial?

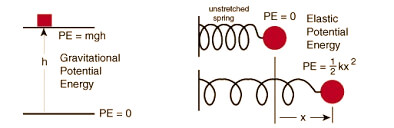
Rumus fisika standar untuk menghitung energi potensial gravitasi adalah $E_p = m \cdot g \cdot h$. Dalam persamaan ini, $m$ mewakili massa benda dalam kilogram (kg), $g$ adalah percepatan gravitasi (sekitar $9.81 \, \text{m/s}^2$ di Bumi), dan $h$ melambangkan tinggi vertikal dalam meter (m) di atas titik acuan yang dipilih. Karena ini adalah hubungan multiplikatif, energi meningkat secara linear dengan setiap faktor tersebut.

Bagaimana cara mencari energi potensial dalam Joule?

Untuk mendapatkan hasil dalam satuan SI Joule ($J$), Anda harus mengalikan massa dalam kg, gravitasi dalam $\text{m/s}^2$, dan tinggi dalam meter. Satu Joule didefinisikan sebagai usaha yang dilakukan oleh gaya satu Newton yang memindahkan benda sejauh satu meter: $1 \, J = 1 \, \text{N} \cdot \text{m} = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$. Kalkulator kami mengotomatiskan konversi ini untuk memberikan nilai yang akurat secara instan.

Apa satuan dari energi potensial?

Satuan SI resmi untuk energi potensial adalah Joule ($J$). Dalam teknik dan nutrisi, Anda mungkin juga menemukan kilojoule ($1 \, kJ = 1000 \, J$) atau megajoule ($MJ$). Joule adalah satuan universal dalam fisika, yang memungkinkan perbandingan langsung antara energi potensial, energi kinetik, panas, dan usaha listrik dalam hukum kekekalan energi.

Apakah energi potensial tergantung pada lintasan yang ditempuh?

Tidak, energi potensial gravitasi adalah fungsi keadaan dan benar-benar tidak bergantung pada lintasan. Ini berarti tidak masalah apakah benda diangkat lurus ke atas atau dipindahkan melalui jalur yang berkelok-kelok untuk mencapai ketinggiannya. Satu-satunya faktor yang menentukan perubahan energi potensial adalah perpindahan vertikal bersih ($h$) antara titik awal dan posisi akhir.

Bisakah energi potensial bernilai negatif?

Ya, energi potensial bisa bernilai negatif karena selalu diukur relatif terhadap tingkat acuan sembarang ($h = 0$). Jika Anda menetapkan tanah sebagai level nol, benda di dasar sumur sedalam 10 meter akan memiliki energi potensial negatif. Ini menunjukkan secara fisik bahwa usaha positif harus dilakukan pada benda tersebut untuk membawanya kembali ke level acuan.

Bagaimana massa mempengaruhi energi potensial gravitasi?

Energi potensial berbanding lurus dengan massa benda. Jika Anda menggandakan massa sambil menjaga ketinggian dan gravitasi tetap konstan, energi potensial akan berlipat ganda tepat dua kali. Inilah sebabnya mengapa benda berat di ketinggian, seperti air di waduk pegunungan, dapat menyimpan energi dalam jumlah besar untuk pembangkit listrik tenaga air.

Rumus apa yang digunakan kalkulator ini?

Kalkulator ini menggunakan persamaan klasik Newton $E_p = m \cdot g \cdot h$. Metode ini adalah standar global dalam pendidikan fisika dan teknik mesin untuk skenario di dekat permukaan planet di mana gravitasi dianggap konstan. Untuk jarak astronomis, diperlukan rumus gravitasi universal yang lebih kompleks, tetapi mgh sangat akurat untuk penggunaan terestrial.

🔢Rekomendasi Kalkulator Lainnya

Kalkulator Usaha (Work)
Kalkulator Energi Kinetik
Kalkulator Momentum
Catatan: Kalkulator ini dirancang untuk memberikan estimasi yang bermanfaat untuk tujuan informasi. Meskipun kami mengupayakan akurasi, hasil dapat bervariasi berdasarkan hukum setempat dan keadaan individu. Kami menyarankan untuk berkonsultasi dengan penasihat profesional untuk keputusan penting.