Potential Energy Calculator

Calculate the gravitational potential energy (GPE) of an object based on its mass, height, and the local acceleration due to gravity.

Calculation Examples

Calculation Case Result
Mass 10 kg, Height 2 m on Earth PE = 196.2 J
Mass 500 g (0.5 kg), Height 10 m on Earth PE = 49.05 J
Mass 100 kg, Height 5 m on the Moon ($1.62 \, \text{m/s}^2$) PE = 810 J

How to Use the Potential Energy Calculator?

Our gravitational potential energy calculator is designed for precision and ease of use in both academic and professional settings. To begin, enter the mass of the object in kilograms (kg). Next, specify the height in meters (m) relative to your chosen reference point—usually the ground or the lowest point in your physical system. The tool includes a pre-set value for Earth’s gravity, $g = 9.81 \, \text{m/s}^2$, but this can be adjusted for calculations involving other celestial bodies like the Moon ($1.62 \, \text{m/s}^2$) or Mars ($3.71 \, \text{m/s}^2$). Understanding potential energy is crucial for analyzing mechanical systems and energy conservation laws. By inputting consistent SI units, you ensure the output is accurately reflected in Joules ($J$). This tool is an essential resource for verifying homework, designing engineering prototypes, or exploring the physics of motion in real-world scenarios.

Understanding the GPE Formula (mgh)

The calculation of gravitational potential energy is a cornerstone of classical mechanics. The energy an object possesses due to its position in a gravitational field is defined by the formula: $E_p = m \cdot g \cdot h$. In this equation, $m$ represents the mass, $g$ is the gravitational acceleration, and $h$ is the vertical height. This relationship shows that potential energy is directly proportional to all three variables. For instance, doubling the height of an object will exactly double its potential energy. This specific formula, often called the mgh equation, assumes that the gravitational field is constant, which is a highly accurate approximation for objects near a planet's surface. The resulting unit, the Joule ($1 \, J = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$), quantifies the work required to lift the object to that specific height against the force of gravity.Gravitational Potential Energy mgh Diagram

Useful Tips 💡

  • Always define a clear reference point (zero-level) before measuring height to ensure consistency.
  • For high-precision aerospace calculations, account for local variations in Earth's gravity based on latitude.
  • Remember that potential energy is a scalar quantity; it has magnitude but no specific direction.

📋Steps to Calculate

  1. Input the object's mass in kilograms (kg).

  2. Enter the vertical height in meters (m).

  3. Specify the gravitational acceleration (default is $9.81 \, \text{m/s}^2$).

  4. Review the calculated potential energy in Joules (J).

Mistakes to Avoid ⚠️

  1. Using weight instead of mass; remember that weight is mass multiplied by the acceleration due to gravity, not just mass itself.
  2. Mixing metric and imperial units, for example using feet for height while applying 9.81 m/s² for gravitational acceleration.
  3. Ignoring the choice of reference level for height, which leads to incorrect calculations of change in potential energy.
  4. Applying the formula to astronomical distances where gravity follows the inverse-square law instead of being constant.

Practical Applications of Potential Energy📊

  1. Calculating the stored energy in hydroelectric dam reservoirs before conversion to electricity.

  2. Analyzing the safety and mechanics of roller coasters and elevators.

  3. Evaluating the impact force of falling objects in construction and safety engineering.

  4. Solving complex physics problems involving the conservation of mechanical energy ($ME = PE + KE$).

Questions and Answers

What is the formula for potential energy?

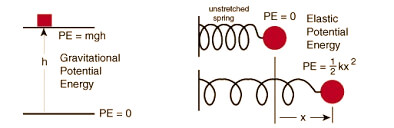
The standard physical formula for calculating gravitational potential energy is $E_p = m \cdot g \cdot h$. In this equation, $m$ represents the mass of the object in kilograms (kg), $g$ is the acceleration due to gravity (approximately $9.81 \, \text{m/s}^2$ on Earth), and $h$ stands for the vertical height in meters (m) above a chosen reference point. Since this is a purely multiplicative relationship, the energy increases linearly with each of these factors.

How do you find potential energy in Joules?

To obtain a result in the SI unit Joules ($J$), you must multiply the mass in kg, the gravity in $\text{m/s}^2$, and the height in meters. A Joule is defined as the work done by a force of one Newton moving an object one meter: $1 \, J = 1 \, \text{N} \cdot \text{m} = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$. Our calculator automates this conversion to provide an immediate and accurate value.

What is the unit of potential energy?

The official SI unit for potential energy is the Joule ($J$). In engineering and nutrition, you might also encounter kilojoules ($1 \, kJ = 1000 \, J$) or megajoules ($MJ$). The Joule is a universal unit in physics, allowing for direct comparison between potential energy, kinetic energy, heat, and electrical work within the law of conservation of energy.

Does potential energy depend on the path taken?

No, gravitational potential energy is a state function and is strictly path-independent. This means it does not matter if an object was lifted straight up or moved along a complex zigzag ramp to reach its height. The only factor that determines the change in potential energy is the net vertical displacement ($h$) between the starting point and the final position.

Can potential energy be negative?

Yes, potential energy can be negative because it is always measured relative to an arbitrary reference level ($h = 0$). If you define the ground as the zero-level, an object at the bottom of a 10-meter well will have negative potential energy. This indicates that positive work must be performed on the object to bring it back up to the reference level.

How does mass affect gravitational potential energy?

Potential energy is directly proportional to the mass of the object. If you double the mass while keeping the height and gravity constant, the potential energy will exactly double. This is why heavy objects at high altitudes, such as water in mountain reservoirs, can store massive amounts of energy for hydroelectric power generation.

What formula does this potential energy calculator use?

This calculator uses the classical Newtonian equation $E_p = m \cdot g \cdot h$. This method is the global standard in physics education and mechanical engineering for scenarios near a planet's surface where gravity is assumed to be constant. For astronomical distances, a more complex general relativity or universal gravitation formula would be required, but $mgh$ is perfectly accurate for terrestrial use.

🔢Try More Calculators

Work Calculator
Kinetic Energy Calculator
Momentum Calculator
Disclaimer: This calculator is designed to provide helpful estimates for informational purposes. While we strive for accuracy, financial (or medical) results can vary based on local laws and individual circumstances. We recommend consulting with a professional advisor for critical decisions.