Calculadora de Energia Potencial

Calcule a energia potencial gravitacional (GPE) de um objeto com base na sua massa, altura e aceleração da gravidade local.

Exemplos de Cálculo

Caso de Cálculo Resultado
Massa 10 kg, Altura 2 m na Terra EP = 196.2 J
Massa 500 g (0.5 kg), Altura 10 m na Terra EP = 49.05 J
Massa 100 kg, Altura 5 m na Lua ($1.62 \, \text{m/s}^2$) EP = 810 J

Como usar a calculadora de energia potencial?

A nossa calculadora de energia potencial gravitacional foi desenvolvida para precisão em contextos académicos e profissionais. Para começar, insira a massa do objeto em quilogramas (kg). Em seguida, especifique a altura em metros (m) em relação ao seu ponto de referência — geralmente o solo ou o ponto mais baixo do sistema. A ferramenta inclui o valor padrão da gravidade na Terra, $g = 9.81 \, \text{m/s}^2$, mas pode ser ajustado para cálculos noutros corpos celestes como a Lua ($1.62 \, \text{m/s}^2$) ou Marte ($3.71 \, \text{m/s}^2$). Compreender a energia potencial é fundamental para analisar sistemas mecânicos e leis de conservação de energia. Ao inserir unidades consistentes do SI, garante que o resultado seja refletido corretamente em Joules ($J$). Esta ferramenta é essencial para verificar trabalhos de casa ou projetar protótipos de engenharia.

Entendendo a Fórmula GPE (mgh)

O cálculo da energia potencial gravitacional é um pilar da mecânica clássica. A energia que um objeto possui devido à sua posição num campo gravitacional é definida pela fórmula: $E_p = m \cdot g \cdot h$. Nesta equação, $m$ representa a massa, $g$ é a aceleração gravitacional e $h$ é a altura vertical. Esta relação mostra que a energia potencial é diretamente proporcional às três variáveis. Por exemplo, duplicar a altura de um objeto duplicará exatamente a sua energia potencial. Esta fórmula assume que o campo gravitacional é constante, o que é uma aproximação altamente precisa perto da superfície de um planeta. A unidade resultante, o Joule ($1 \, J = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$), quantifica o trabalho necessário para elevar o objeto a essa altura específica contra a força da gravidade.Diagrama de Energia Potencial Gravitacional mgh

Dicas Úteis 💡

  • Defina sempre um ponto de referência claro (nível zero) antes de medir a altura para garantir consistência.
  • Para cálculos aeroespaciais de alta precisão, considere variações locais da gravidade baseadas na latitude.
  • Lembre-se que a energia potencial é uma grandeza escalar; tem magnitude mas não direção.

📋Passos para Calcular

  1. Insira a massa do objeto em quilogramas (kg).

  2. Introduza a altura vertical em metros (m).

  3. Especifique a aceleração gravitacional (padrão $9.81 \, \text{m/s}^2$).

  4. Verifique a energia potencial calculada em Joules (J).

Erros a evitar ⚠️

  1. Usar o peso em vez da massa; lembre-se que o peso é a massa multiplicada pela aceleração da gravidade, não apenas a massa em si.
  2. Misturar unidades métricas e imperiais, por exemplo, usar pés para a altura enquanto se aplica 9,81 m/s² para a aceleração gravitacional.
  3. Ignorar a escolha do nível de referência para a altura, o que leva a cálculos incorretos da variação da energia potencial.
  4. Aplicar a fórmula a distâncias astronómicas onde a gravidade segue a lei do inverso do quadrado em vez de ser constante.

Aplicações Práticas da Energia Potencial📊

  1. Calcular a energia armazenada em reservatórios de barragens hidroelétricas antes da conversão.

  2. Analisar a segurança e mecânica de montanhas-russas e elevadores.

  3. Avaliar a força de impacto de objetos em queda na engenharia de segurança e construção.

  4. Resolver problemas complexos de física envolvendo a conservação da energia mecânica ($EM = EP + EC$).

Perguntas e Respostas

Qual é a fórmula da energia potencial?

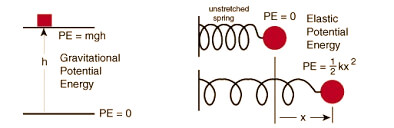
A fórmula física padrão para calcular a energia potencial gravitacional é $E_p = m \cdot g \cdot h$. Nesta equação, $m$ representa a massa do objeto em quilogramas (kg), $g$ é a aceleração da gravidade (cerca de $9.81 \, \text{m/s}^2$ na Terra) e $h$ é a altura vertical em metros (m) acima de um ponto de referência escolhido. Como é uma relação puramente multiplicativa, a energia aumenta linearmente com cada um destes fatores.

Como calcular a energia potencial em Joules?

Para obter o resultado em Joules ($J$), a unidade do SI, deve multiplicar a massa em kg, a gravidade em $\text{m/s}^2$ e a altura em metros. Um Joule é definido como o trabalho realizado por uma força de um Newton ao deslocar um objeto por um metro: $1 \, J = 1 \, \text{N} \cdot \text{m} = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$. O nosso calculador automatiza esta conversão para fornecer um valor exato instantaneamente.

Qual é a unidade de energia potencial?

A unidade oficial do Sistema Internacional (SI) para a energia potencial é o Joule ($J$). Em engenharia e nutrição, poderá também encontrar quilojoules ($1 \, kJ = 1000 \, J$) ou megajoules ($MJ$). O Joule é uma unidade universal na física, permitindo a comparação direta entre energia potencial, energia cinética, calor e trabalho mecânico dentro da lei da conservação da energia.

A energia potencial depende do caminho percorrido?

Não, a energia potencial gravitacional é uma função de estado e é estritamente independente do caminho. Isto significa que não importa se um objeto foi elevado verticalmente ou movido através de uma rampa em ziguezague; o que determina a variação da energia potencial é apenas o deslocamento vertical líquido ($h$) entre o ponto inicial e a posição final.

A energia potencial pode ser negativa?

Sim, a energia potencial pode ser negativa porque é sempre medida em relação a um nível de referência arbitrário ($h = 0$). Se definir o solo como o nível zero, um objeto no fundo de um poço terá energia potencial negativa. Isto indica fisicamente que deve ser realizado trabalho positivo sobre o objeto para o trazer de volta ao nível de referência.

Como a massa afeta a energia potencial?

A energia potencial é diretamente proporcional à massa do objeto. Se duplicar a massa mantendo a altura e a gravidade constantes, a energia potencial irá duplicar exatamente. É por isso que objetos pesados em grandes altitudes, como a água em albufeiras de barragens, podem armazenar quantidades massivas de energia para geração hidroelétrica.

Que fórmula utiliza esta calculadora?

Esta calculadora utiliza a equação clássica de Newton $E_p = m \cdot g \cdot h$. Este método é o padrão global no ensino da física e engenharia mecânica para cenários próximos da superfície terrestre, onde a gravidade é assumida como constante. Para distâncias astronómicas, seria necessária uma fórmula de gravitação universal, mas a mgh é perfeitamente precisa para uso terrestre.

🔢Experimente Mais Calculadoras

Calculadora de Trabalho
Calculadora de Energia Cinética
Calculadora de Momento
Nota: Esta calculadora foi projetada para fornecer estimativas úteis para fins informativos. Embora nos esforcemos pela precisão, os resultados podem variar com base nas leis locais e circunstâncias individuais. Recomendamos consultar um consultor profissional para decisões críticas.