Calcolatore Energia Potenziale

Determina l'energia potenziale gravitazionale (GPE) di un oggetto in base alla sua massa, altezza e accelerazione di gravità.

Esempi di calcolo

Caso di calcolo Risultato
Massa 10 kg, Altezza 2 m sulla Terra E_p = 196.2 J
Sasso di 500 g (0.5 kg), Altezza 10 m sulla Terra E_p = 49.05 J
Massa 100 kg, Altezza 5 m sulla Luna ($1.62 \, \text{m/s}^2$) E_p = 810 J

Come usare il calcolatore di energia potenziale?

Il nostro calcolatore di energia potenziale è progettato per garantire precisione in ambito scolastico e professionale. Inserisci la massa dell'oggetto in chilogrammi (kg), quindi specifica l'altezza in metri (m) rispetto a un punto di riferimento (solitamente il suolo). Lo strumento preimposta la gravità terrestre a $g = 9.81 \, \text{m/s}^2$, ma puoi modificarla per calcoli su altri corpi celesti come la Luna ($1.62 \, \text{m/s}^2$). Comprendere l'energia potenziale è fondamentale per analizzare i sistemi meccanici e la conservazione dell'energia. Utilizzando unità di misura del SI coerenti, otterrai il risultato espresso correttamente in Joule ($J$). È una risorsa essenziale per verificare compiti di fisica o progettare modelli ingegneristici.

Spiegazione della Formula mgh

Il calcolo dell'energia potenziale gravitazionale è un concetto base della meccanica classica. L'energia di un corpo dovuta alla sua posizione è definita dalla formula: $E_p = m \cdot g \cdot h$. In questa equazione, $m$ rappresenta la massa, $g$ l'accelerazione di gravità e $h$ l'altezza verticale. Questa relazione indica che l'energia è direttamente proporzionale a tutte e tre le variabili. Ad esempio, raddoppiare l'altezza di un oggetto raddoppierà esattamente la sua energia potenziale. Questa formula presuppone che il campo gravitazionale sia costante, un'approssimazione valida vicino alla superficie terrestre. L'unità risultante, il Joule ($1 \, J = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$), quantifica il lavoro necessario per sollevare l'oggetto contro la forza di gravità.Diagramma Energia Potenziale mgh

Suggerimenti utili 💡

  • Scegli sempre un punto di riferimento zero chiaro per l'altezza per evitare errori.
  • Per calcoli aerospaziali, considera le variazioni locali di $g$ basate sulla latitudine.
  • L'energia potenziale è una grandezza scalare (non ha una direzione).

📋Passaggi per Calcolare

  1. Inserisci la massa dell'oggetto in chilogrammi (kg).

  2. Inserisci l'altezza verticale in metri (m).

  3. Specifica l'accelerazione di gravità (default $9.81 \, \text{m/s}^2$).

  4. Visualizza l'energia potenziale in Joule (J).

Errori comuni ⚠️

  1. Usare il peso al posto della massa; ricorda che il peso è la massa moltiplicata per l’accelerazione di gravità, non solo la massa stessa.
  2. Mischiare unità metriche e imperiali, ad esempio usando i piedi per l’altezza mentre si applica 9,81 m/s² per l’accelerazione di gravità.
  3. Ignorare la scelta del livello di riferimento per l’altezza, il che porta a calcoli errati della variazione dell’energia potenziale.
  4. Applicare la formula a distanze astronomiche dove la gravità segue la legge dell’inverso del quadrato invece di essere costante.

Applicazioni pratiche dell'energia potenziale📊

  1. Calcolare l'energia accumulata nelle dighe idroelettriche prima della trasformazione.

  2. Analizzare la sicurezza di montagne russe e ascensori.

  3. Valutare la forza d'impatto di oggetti in caduta nell'ingegneria civile.

  4. Risolvere problemi sulla conservazione dell'energia meccanica ($E_m = E_p + E_c$).

Domande Frequenti

Qual è la formula dell'energia potenziale?

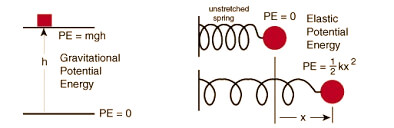
La formula matematica standard per calcolare l'energia potenziale gravitazionale è $E_p = m \cdot g \cdot h$. In questa espressione, $m$ indica la massa del corpo in chilogrammi (kg), $g$ rappresenta l'accelerazione di gravità (circa $9.81 \, \text{m/s}^2$ sulla Terra) e $h$ è l'altezza verticale in metri (m) rispetto a un piano di riferimento scelto. La formula esprime come l'energia accumulata dipenda linearmente dalla massa e dalla posizione dell'oggetto nel campo gravitazionale.

Come si trova l'energia in Joule?

Per ottenere un valore espresso in Joule ($J$), è necessario moltiplicare la massa per l'accelerazione di gravità e per l'altezza, assicurandosi che tutte le unità appartengano al Sistema Internazionale. Un Joule è definito come il lavoro svolto da una forza di un Newton che sposta un corpo di un metro: $1 \, J = 1 \, \text{N} \cdot \text{m}$. Il nostro calcolatore esegue automaticamente questo prodotto per fornirti un risultato immediato e preciso.

Qual è l'unità dell'energia potenziale?

L'unità di misura ufficiale nel Sistema Internazionale (SI) è il Joule ($J$). Nel linguaggio tecnico si utilizzano spesso i suoi multipli, come il chilojoule ($1 \, kJ = 1000 \, J$) o il megajoule ($MJ$). Il Joule è un'unità versatile che permette di confrontare l'energia potenziale con altre forme di energia, come quella cinetica o termica, facilitando lo studio dei principi di conservazione.

L'energia potenziale dipende dal percorso?

No, l'energia potenziale gravitazionale è una funzione di stato e gode della proprietà di essere indipendente dal percorso seguito (proprietà delle forze conservative). Non importa se un oggetto viene sollevato verticalmente o lungo un piano inclinato: se la quota finale raggiunta è la stessa, l'energia potenziale acquisita sarà identica, dipendendo solo dal dislivello verticale ($h$).

L'energia potenziale può essere negativa?

Sì, l'energia potenziale può assumere valori negativi a seconda di dove viene posizionato lo "zero" di riferimento. Se fissi il livello del suolo come zero ($h = 0$), un oggetto situato in un seminterrato avrà un'energia potenziale negativa. Questo valore indica semplicemente che è necessario compiere del lavoro positivo per riportare l'oggetto al livello di riferimento.

In che modo la massa influisce sull'energia?

L'energia potenziale è direttamente proporzionale alla massa dell'oggetto. Questo significa che, a parità di altezza e gravità, un oggetto con massa doppia avrà un'energia potenziale esattamente doppia. Questo principio è fondamentale in ingegneria per calcolare, ad esempio, l'energia immagazzinata nei pesi di un orologio a pendolo o nelle masse di un ascensore.

Che formula usa questo calcolatore?

Il calcolatore applica rigorosamente l'equazione classica $E_p = m \cdot g \cdot h$. Questo metodo rappresenta lo standard globale nella fisica newtoniana ed è perfetto per applicazioni sulla superficie terrestre. Per calcoli che coinvolgono altezze orbitale o distanze interplanetarie, sarebbe necessario considerare la variazione della gravità, ma per scopi didattici e professionali comuni, questa formula è estremamente accurata.

🔢Prova Altri Calcolatori

Calcolatore Lavoro
Calcolatore di Energia Cinetica
Calcolatore di Momento
Nota: Questo calcolatore è progettato per fornire stime utili a scopo informativo. Sebbene ci sforziamo di garantire l'accuratezza, i risultati possono variare in base alle leggi locali e alle circostanze individuali. Si consiglia di consultare un consulente professionale per decisioni importanti.