Máy Tính Thế Năng
Tính thế năng hấp dẫn (GPE) của một vật dựa trên khối lượng, độ cao và gia tốc trọng trường tại địa phương.
Ví dụ tính toán
📋Các bước tính toán
-
Nhập khối lượng của vật bằng kilôgam (kg).
-
Nhập chiều cao thẳng đứng bằng mét (m).
-
Xác định gia tốc trọng trường (mặc định là $9.81 \, \text{m/s}^2$).
-
Xem kết quả thế năng đã tính bằng Joule (J).
Những lỗi cần tránh ⚠️
- Sử dụng trọng lượng thay vì khối lượng; hãy nhớ rằng trọng lượng là khối lượng nhân với gia tốc trọng trường, chứ không chỉ là bản thân khối lượng.
- Trộn lẫn các đơn vị hệ mét và hệ Anh, ví dụ như sử dụng feet cho chiều cao trong khi áp dụng 9,81 m/s² cho gia tốc trọng trường.
- Bỏ qua việc chọn mức tham chiếu cho chiều cao, dẫn đến tính toán sai lệch về sự thay đổi thế năng.
- Áp dụng công thức cho khoảng cách thiên văn nơi trọng lực tuân theo định luật nghịch đảo bình phương thay vì là hằng số.
Ứng dụng thực tế của thế năng📊
Tính toán năng lượng dự trữ trong các hồ chứa thủy điện (như thủy điện Sơn La) trước khi chuyển hóa thành điện năng.
Phân tích tính an toàn và cơ chế hoạt động của tàu lượn siêu tốc và thang máy.
Đánh giá lực va đập của các vật rơi trong kỹ thuật xây dựng và an toàn lao động.
Giải các bài toán vật lý phức tạp về bảo toàn cơ năng ($E = W_t + W_d$).
Câu hỏi và Trả lời
Công thức tính thế năng là gì?
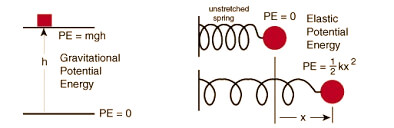
Công thức vật lý tiêu chuẩn để tính thế năng hấp dẫn là $E_p = m \cdot g \cdot h$. Trong đó, $m$ là khối lượng của vật tính bằng kilôgam (kg), $g$ là gia tốc trọng trường (khoảng $9.81 \, \text{m/s}^2$ trên Trái đất) và $h$ là độ cao thẳng đứng tính bằng mét (m) so với một mốc thế năng đã chọn. Công thức này cho thấy năng lượng tích lũy phụ thuộc tuyến tính vào cả ba đại lượng này.
Làm thế nào để tìm thế năng bằng Joule?
Để nhận được kết quả tính bằng đơn vị Joule ($J$), bạn cần thực hiện phép nhân giữa khối lượng, trọng lực và chiều cao với điều kiện tất cả các đơn vị đầu vào phải theo hệ đo lường quốc tế (SI). Một Joule được định nghĩa là công thực hiện khi một lực có độ lớn 1 Newton làm dịch chuyển vật một khoảng cách 1 mét: $1 \, J = 1 \, \text{kg} \cdot \text{m}^2/\text{s}^2$. Máy tính của chúng tôi sẽ tự động xử lý các phép tính này một cách nhanh chóng.
Đơn vị của thế năng là gì?
Đơn vị đo lường chính thức trong hệ SI cho thế năng là Joule ($J$). Trong đời sống và kỹ thuật, chúng ta cũng thường sử dụng kilojoule ($1 \, kJ = 1000 \, J$) hoặc megajoule ($MJ$) để biểu thị các giá trị năng lượng lớn hơn. Joule là đơn vị vạn năng trong vật lý, cho phép so sánh thế năng với các dạng năng lượng khác như động năng hay nhiệt năng.
Thế năng có phụ thuộc vào quỹ đạo chuyển động không?
Không, thế năng hấp dẫn có một tính chất đặc biệt là không phụ thuộc vào đường đi mà vật đã di chuyển. Cho dù bạn nâng một vật thẳng đứng hay kéo nó dọc theo một mặt phẳng nghiêng để đạt cùng một độ cao, thế năng cuối cùng vẫn như nhau. Nó chỉ phụ thuộc vào sự chênh lệch độ cao thẳng đứng ($h$) giữa điểm đầu và điểm cuối so với mốc thế năng.
Thế năng có thể âm không?
Có, giá trị của thế năng có thể âm tùy thuộc vào việc bạn chọn mốc thế năng ($h = 0$) ở đâu. Nếu bạn chọn mặt đất làm mốc, một vật nằm dưới giếng sâu sẽ có thế năng âm. Điều này đơn giản có nghĩa là cần phải cung cấp một công dương để đưa vật đó trở lại mức mốc thế năng ban đầu.
Khối lượng ảnh hưởng thế nào đến thế năng?
Thế năng tỉ lệ thuận trực tiếp với khối lượng của vật. Điều này có nghĩa là nếu bạn giữ nguyên độ cao và trọng lực nhưng tăng gấp đôi khối lượng, thế năng của vật cũng sẽ tăng gấp đôi. Đây là lý do tại sao các vật thể có khối lượng lớn tích trữ một lượng năng lượng khổng lồ ngay cả ở độ cao thấp, một yếu tố cực kỳ quan trọng trong kỹ thuật xây dựng và an toàn.
Máy tính này sử dụng phương pháp nào?
Máy tính của chúng tôi áp dụng chính xác phương trình mgh cổ điển của Newton: $E_p = m \cdot g \cdot h$. Đây là phương pháp chuẩn mực được công nhận trên toàn thế giới trong giáo dục khoa học và kỹ thuật cơ khí. Đối với các ứng dụng liên quan đến độ cao quỹ đạo hoặc khoảng cách giữa các hành tinh, cần sử dụng công thức vạn vật hấp dẫn phức tạp hơn, nhưng mgh là hoàn hảo cho các ứng dụng thực tế gần bề mặt Trái đất.
Lưu ý: Máy tính này được thiết kế để cung cấp các ước tính hữu ích cho mục đích thông tin. Mặc dù chúng tôi nỗ lực vì sự chính xác, kết quả có thể thay đổi tùy thuộc vào luật địa phương và hoàn cảnh cá nhân. Chúng tôi khuyên bạn nên tham khảo ý kiến của cố vấn chuyên môn cho các quyết định quan trọng.