Calculadora de Queda Livre
Analise o movimento de um objeto em queda sob a influência exclusiva da gravidade. Calcule velocidade, tempo e distância com precisão.
Método de cálculo (passo a passo)
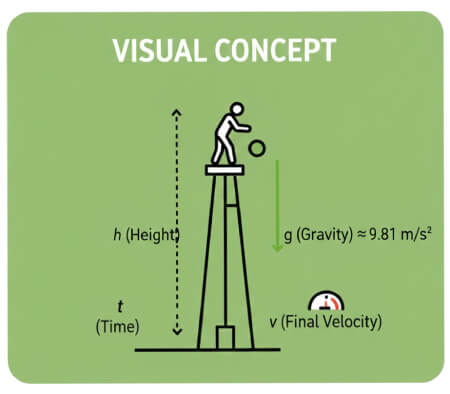
Suposições: velocidade inicial zero, sem resistência do ar. Equações cinemáticas usadas:
- h = ½ g t² — altura / distância percorrida
- v = g t — velocidade final no impacto
- t = √(2h / g) — tempo de queda
- h = v² / (2g) — altura a partir da velocidade
- t = v / g — tempo a partir da velocidade
Aceleração da gravidade: g = 9.81 m/s²
Exemplos de Cálculo
Como usar a calculadora de queda livre?
Para utilizar a calculadora de queda livre, defina as suas variáveis cinemáticas conhecidas. Selecione o parâmetro pretendido: duração da queda ($t$), velocidade de impacto final ($v$) or deslocamento total ($d$). Insira os dados nos campos respetivos; para uma queda padrão a partir do repouso, certifique-se de que a velocidade inicial ($v_0$) é zero. Escolha o seu sistema de unidades preferido—Métrico ($m, s$) ou Imperial ($ft, s$). O algoritmo aplica a aceleração padrão da gravidade ($g \approx 9.81 \text{ m/s}^2$ ou $32.2 \text{ ft/s}^2$). Ao clicar em "Calcular", o sistema executa as equações cinemáticas para fornecer resultados instantâneos, incluindo passos intermédios para clareza pedagógica. Esta ferramenta é otimizada para a mecânica newtoniana onde a resistência do ar é desprezível.
Enquadramento Matemático e Equações Cinemáticas
A queda livre é definida como um movimento retilíneo com aceleração constante. No vácuo ou ignorando o arrasto aerodinâmico, o movimento é regido pelas seguintes equações fundamentais: 1. Deslocamento: $d = \frac{1}{2}gt^2$ | 2. Velocidade Final: $v = gt$ | 3. Relação Velocidade-Deslocamento: $v = \sqrt{2gd}$. Onde $g$ representa a intensidade do campo gravítico local. Estas derivações assumem que o objeto parte de um estado de repouso ($v_0 = 0$). Em meios fluídos (como o ar), os objetos acabam por atingir a velocidade terminal devido às forças de arrasto, um fator não contabilizado neste modelo newtoniano simplificado.
Dicas Úteis 💡
- Garanta que a velocidade inicial é zero para cenários de queda pura a partir do repouso.
- Utilize unidades consistentes para evitar erros de conversão nos resultados.
📋Passos para Calcular
-
Selecione a variável conhecida (altura, duração ou velocidade).
-
Especifique o sistema de unidades (Métrico ou Imperial).
-
Execute o cálculo para obter dados cinemáticos completos.
Erros a evitar ⚠️
- Ignorar os efeitos da resistência do ar em objetos com elevada área de superfície em relação à massa.
- Confundir massa com peso; no vácuo, todos os objetos caem à mesma taxa independentemente da massa.
- Medições de tempo imprecisas em experiências manuais que levam a erros exponenciais na distância.
- Aplicar estas equações a velocidades relativistas ou campos gravíticos não uniformes.
Aplicações Práticas📊
Cálculo da energia de impacto e velocidade para avaliações de segurança estrutural.
Verificação de dados experimentais em sessões de laboratório de mecânica clássica.
Estimativa da altura de estruturas verticais com base em quedas cronometradas.
Modelação de trajetória inicial para lançamento de cargas ou física de drones.