Serbest Düşüş Hesaplayıcı

Sadece yerçekimi etkisi altında düşen bir nesnenin hareketini analiz edin.

Yükseklik / Düşülen mesafe (m): Düşme süresi (s): Son hız (m/s): Yerçekimi ivmesi g (m/s²):

Hesaplama yöntemi (adım adım)

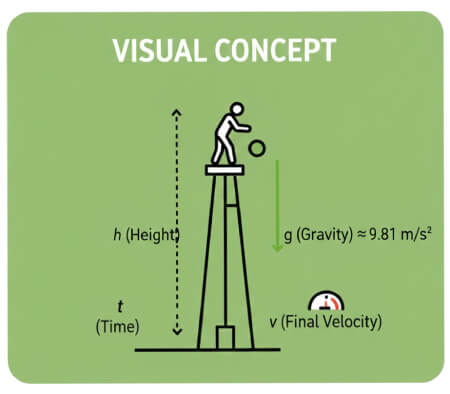
Varsayımlar: sıfır başlangıç hızı, hava direnci yok. Kullanılan kinematik denklemler:

h = ½ g t² — yükseklik / düşülen mesafe
v = g t — çarpma anındaki son hız
t = √(2h / g) — düşme süresi
h = v² / (2g) — hızdan yükseklik
t = v / g — hızdan süre

Yerçekimi ivmesi: g = 9.81 m/s²

Tam olarak birini girin: yükseklik, süre veya hız. g değeri yukarıdan ayarlanabilir.

Hesaplama Örnekleri

Hesaplama Durumu	Sonuç
Galata Kulesi'nden serbest bırakılan nesne ($63 \text{ m}$)	$t \approx 3.58 \text{ s}, v \approx 35.15 \text{ m/s}$
150 fit yükseklikten bırakma (Imperial birimler, $g = 32.2 \text{ ft/s}^2$)	$t \approx 3.05 \text{ s}, v \approx 98.28 \text{ ft/s}$
10 saniye süren serbest düşüş mesafesi	$d \approx 490.5 \text{ m}, v \approx 98.1 \text{ m/s}$

Serbest Düşüş Hesaplayıcısı nasıl kullanılır?

Hedef parametreyi seçin: düşüş süresi ($t$), son hız ($v$) veya toplam mesafe ($d$). Bilinen verileri ilgili alanlara girin; durgun halden düşüş için ilk hızın ($v_0$) sıfır olduğundan emin olun. Tercih ettiğiniz birim sistemini seçin—Metrik ($m, s$) veya Imperial ($ft, s$). Algoritma standart yerçekimi ivmesini ($g \approx 9.81 \text{ m/s}^2$ veya $32.2 \text{ ft/s}^2$) uygular. "Hesapla" butonuna bastığınızda, sistem kinematik denklemleri çalıştırarak anlık sonuçlar üretir. Bu araç, hava direncinin ihmal edilebilir olduğu Newton mekaniği için optimize edilmiştir.

Matematiksel Çerçeve ve Kinematik Denklemler

Serbest düşüş, sabit ivmeli doğrusal bir hareket olarak tanımlanır. Vakum ortamında veya hava direnci ihmal edildiğinde hareket şu temel denklemlerle yönetilir: 1. Yer Değiştirme: $d = \frac{1}{2}gt^2$ | 2. Son Hız: $v = gt$ | 3. Hız-Mesafe İlişkisi: $v = \sqrt{2gd}$. Burada $g$ yerel yerçekimi alanını temsil eder. Bu türetmeler nesnenin durgun halden başladığını ($v_0 = 0$) varsayar. Hava gibi akışkan ortamlarda, nesneler sürükleme kuvveti nedeniyle terminal hıza ulaşır; bu faktör bu basitleştirilmiş modelde dikkate alınmaz. Serbest Düşüş Dinamiği

Uzman Tavsiyeleri 💡

Durgun halden düşüş senaryoları için ilk hızın sıfır olduğundan emin olun.
Hatalı sonuçlardan kaçınmak için tüm alanlarda tutarlı birimler kullanın.

📋Hesaplama Adımları

Bilinen değişkeni seçin (yükseklik, süre veya hız).
Birim sistemini (Metrik veya Imperial) belirleyin.
Kapsamlı kinematik verileri almak için hesaplamayı çalıştırın.

Kaçınılması Gereken Hatalar ⚠️

Yüzey alanı/kütle oranı yüksek nesnelerde hava direncini ihmal etmek.
Kütle ve ağırlığı karıştırmak; vakumda tüm nesneler kütleden bağımsız olarak aynı hızda düşer.
Manuel deneylerde mesafede eksponansiyel hatalara yol açan hatalı zaman ölçümleri.
Bu denklemleri rölativistik hızlara veya düzgün olmayan yerçekimi alanlarına uygulamak.

Pratik Uygulamalar📊

Yapısal güvenlik değerlendirmeleri için çarpma enerjisi ve hızı hesaplama.
Klasik mekanik laboratuvar derslerinde deneysel verilerin doğrulanması.
Zamanlanmış düşüşler yardımıyla dikey yapıların yüksekliğini tahmin etme.
Drone ve yük bırakma sistemleri için temel yörünge modelleme.

Sıkça Sorulan Sorular (SSS)

Serbest düşüşün tanımı nedir?

Newton fiziğinde serbest düşüş, bir cismin sadece yerçekimi kuvveti etkisi altında yaptığı harekettir. Bu, hava direncinin olmadığı bir vakum ortamını ifade eder. Bu koşullarda cisim, kütlesinden bağımsız olarak yerin merkezine doğru yaklaşık $g \approx 9.81 \text{ m/s}^2$ sabit ivme ile hızlanır.

Belirli bir yükseklikten düşüş süresi nasıl hesaplanır?

$d = \frac{1}{2}gt^2$ denkleminden süreyi $t = \sqrt{2d/g}$ olarak buluruz. Bu hesaplama cismin ilk hızının sıfır olduğunu varsayar. Örneğin 100 metreden düşüş yaklaşık 4.52 saniye sürer.

Son hız formülü nedir?

Çarpma anındaki hız, süre veya mesafeye göre belirlenir. Süre biliniyorsa $v = gt$, mesafe biliniyorsa $v = \sqrt{2gd}$ formülü kullanılır.

Bu araç hava direncini hesaba katıyor mu?

Hayır, bu hesaplayıcı vakum ortamını varsayan "ideal" serbest düşüş için tasarlanmıştır. Gerçek dünyada hava direnci hızı sınırlayarak terminal hıza ulaşılmasına neden olur.

Hesaplama için nesnenin kütlesi gerekiyor mu?

Hayır. Eşdeğerlik ilkesine göre kütle vakumdaki düşüş hızını etkilemez. Gravitasyonel kütle ve eylemsizlik kütlesi birbirini götürür ($ma = mg$).

Yerçekimi için hangi sabit kullanılır?

Hesaplayıcı, metrik sistemde $g_n = 9.80665 \text{ m/s}^2$, imperial sistemde ise yaklaşık $32.174 \text{ ft/s}^2$ değerini kullanır.

Not: Bu hesaplayıcı, bilgilendirme amaçlı faydalı tahminler sunmak için tasarlanmıştır. Doğruluk için çaba göstersek de sonuçlar yerel yasalara ve bireysel durumlara göre değişiklik gösterebilir. Önemli kararlar için profesyonel bir danışmana başvurmanızı öneririz.