Calculadora de Caída Libre

Analice el movimiento de un objeto que cae bajo la única influencia de la gravedad.

Método de cálculo (paso a paso)

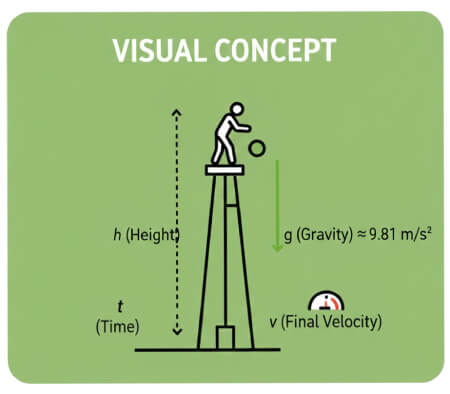
Suposiciones: velocidad inicial cero, sin resistencia del aire. Ecuaciones cinemáticas usadas:

  • h = ½ g t² — altura / distancia caída
  • v = g t — velocidad final al impacto
  • t = √(2h / g) — tiempo de caída
  • h = v² / (2g) — altura desde la velocidad
  • t = v / g — tiempo desde la velocidad

Aceleración debida a la gravedad: g = 9.81 m/s²

Ingrese exactamente uno de: altura, tiempo o velocidad. El valor de g se puede ajustar arriba.

¿Te ha resultado útil esta calculadora?

★ ★ ★ ★ ★
4.9/5 (19 votos)

Ejemplos de cálculo

Caso de cálculo Resultado
Objeto caído desde la Sagrada Familia ($172 \text{ m}$) en reposo $t \approx 5.92 \text{ s}, v \approx 58.08 \text{ m/s}$
Altura de liberación de $200 \text{ pies}$ (Unidades imperiales, $g = 32.2 \text{ ft/s}^2$) $t \approx 3.52 \text{ s}, v \approx 113.44 \text{ ft/s}$
Duración de caída de $8 \text{ segundos}$ desde gran altitud $d \approx 313.92 \text{ m}, v \approx 78.48 \text{ m/s}$

¿Cómo utilizar la calculadora de caída libre?

Seleccione el parámetro objetivo: duración de la caída ($t$), velocidad de impacto final ($v$) o desplazamiento total ($d$). Ingrese los datos en los campos respectivos; para una caída estándar desde el reposo, asegúrese de que la velocidad inicial ($v_0$) sea cero. Elija su sistema de unidades preferido: Métrico ($m, s$) o Imperial ($ft, s$). El algoritmo aplica la aceleración estándar de la gravedad ($g \approx 9.81 \text{ m/s}^2$ o $32.2 \text{ ft/s}^2$). Al hacer clic en "Calcular", el sistema ejecuta las ecuaciones cinemáticas para proporcionar resultados instantáneos, incluyendo pasos intermedios para mayor claridad pedagógica. Esta herramienta está optimizada para la mecánica newtoniana donde la resistencia del aire es despreciable, siendo ideal para demostraciones educativas, aproximaciones de ingeniería y resolución de problemas físicos.

Marco Matemático y Ecuaciones Cinemáticas

La caída libre se define como un movimiento rectilíneo con aceleración constante. En el vacío o ignorando el arrastre aerodinámico, el movimiento se rige por las siguientes ecuaciones fundamentales: 1. Desplazamiento: $d = \frac{1}{2}gt^2$ | 2. Velocidad Final: $v = gt$ | 3. Relación Velocidad-Desplazamiento: $v = \sqrt{2gd}$. Donde $g$ representa la intensidad del campo gravitatorio local. Estas derivaciones asumen que el objeto se origina en un estado de reposo ($v_0 = 0$) y experimenta un campo uniforme. En medios fluidos (como el aire), los objetos alcanzan eventualmente una velocidad terminal debido a las fuerzas de arrastre, un factor no incluido en este modelo simplificado.Dinámica de Caída Libre

Guía de Uso y Consejos 💡

  • Asegúrese de que la velocidad inicial sea cero para escenarios de caída pura desde el reposo.
  • Utilice unidades consistentes en todos los campos para evitar errores de conversión.

📋Pasos para Calcular

  1. Seleccione la variable conocida (altura, duración o velocidad).

  2. Especifique el sistema de unidades (Métrico o Imperial).

  3. Ejecute el cálculo para obtener datos cinemáticos completos.

Errores a evitar ⚠️

  1. Ignorar los efectos de la resistencia del aire en objetos con alta relación superficie-masa.
  2. Confundir masa con peso; en el vacío, todos los objetos caen al mismo ritmo sin importar su masa.
  3. Mediciones de tiempo imprecisas en experimentos manuales que causan errores exponenciales en la distancia.
  4. Aplicar estas ecuaciones a velocidades relativistas o campos gravitatorios no uniformes.

Aplicaciones Prácticas📊

  1. Cálculo de la energía de impacto y velocidad para evaluaciones de seguridad estructural.

  2. Verificación de datos experimentales en sesiones de laboratorio de mecánica clásica.

  3. Estimación de la altura de estructuras verticales basada en caídas cronometradas.

  4. Modelado de trayectoria inicial para despliegue de drones y cargas útiles.

Preguntas Frecuentes (FAQ)

¿Qué define exactamente el fenómeno físico de la caída libre?

La caída libre es un movimiento rectilíneo uniformemente acelerado (MRUA) donde la única fuerza actuante es la interacción gravitatoria. En condiciones ideales (vacío), un objeto no experimenta resistencia aerodinámica ni flotabilidad. Bajo este paradigma, la aceleración es constante e independiente de la composición química o la masa del cuerpo, un concepto fundamental de la relatividad general conocido como el Principio de Equivalencia.

¿Cómo calcular el tiempo de tránsito desde una altura determinada?

Utilizamos la ecuación cinemática de posición: $h = \frac{1}{2}g t^2$. Despejando la variable temporal para un objeto que parte del reposo, obtenemos $t = \sqrt{\frac{2h}{g}}$. Esta relación cuadrática implica que para duplicar el tiempo de caída, la altura debe cuadruplicarse. Nuestra calculadora computa estas raíces cuadradas con alta precisión decimal para aplicaciones en balística y laboratorios de física.

¿Cuál es la fórmula para determinar la velocidad final de impacto?

La velocidad de llegada se calcula mediante la Ecuación de Torricelli: $v_f = \sqrt{2 \cdot g \cdot h}$, o en función del tiempo mediante $v_f = g \cdot t$. Estas fórmulas demuestran que la velocidad aumenta de forma lineal con el tiempo pero sigue una progresión de raíz cuadrada respecto al desplazamiento vertical. Es un dato crítico para evaluar la energía de impacto en análisis de seguridad y resistencia de materiales.

¿Por qué la masa no interviene en las ecuaciones de caída libre?

En el vacío, la masa inercial y la masa gravitatoria son idénticas y se cancelan en la ecuación $m \cdot a = m \cdot g$, resultando en $a = g$. Este descubrimiento, atribuido a Galileo y confirmado por la misión Apollo 15, significa que una pluma y un martillo caen a la misma velocidad. Nuestra herramienta respeta esta ley física, permitiendo realizar cálculos universales para cualquier objeto sin necesidad de conocer su peso.

¿Cómo afecta la altitud a la constante de gravedad $g$?

Aunque se suele usar el valor estándar de $9.81 \, \text{m/s}^2$, la gravedad disminuye con la altitud según la ley de gravitación de Newton: $g = \frac{G \cdot M}{r^2}$. Para cálculos de precisión en geodesia o aviación, nuestra herramienta permite ajustar la constante de gravedad local, garantizando que el tiempo de caída sea exacto independientemente de la ubicación geográfica.

¿Qué es la velocidad terminal y por qué difiere de la caída libre?

La caída libre real en la Tierra se ve limitada por la fricción viscosa del aire. Cuando la fuerza de arrastre iguala al peso, el objeto alcanza la velocidad terminal y deja de acelerar. Esta calculadora se enfoca en el modelo de caída libre "ideal", que es el estándar educativo para comprender la aceleración gravitatoria pura antes de introducir variables de dinámica de fluidos.

¿Cómo se aplica la conservación de la energía en estos cálculos?

El movimiento sigue la ley de conservación de la energía mecánica: $E_p = E_k \rightarrow mgh = \frac{1}{2}mv^2$. Al cancelar la masa, vemos que la velocidad depende únicamente de la altura inicial. Esta perspectiva energética es útil para entender cómo la energía potencial gravitatoria se transforma íntegramente en energía cinética antes del contacto con la superficie.

🔢Otras herramientas que podrían interesarte

Calculadora de Fuerza Neta
Calculadora de Energía Potencial
Calculadora de Trabajo
Nota: Esta calculadora está diseñada para ofrecer estimaciones útiles con fines informativos. Aunque nos esforzamos por la precisión, los resultados pueden variar según las leyes locales y las circunstancias individuales. Recomendamos consultar con un asesor profesional para decisiones importantes.