Calculadora de Fuerza Neta
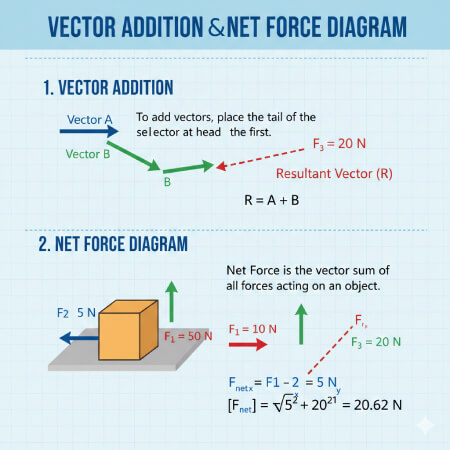
Determine la suma vectorial de todas las fuerzas que actúan sobre un objeto.
Fuerza resultante
Ejemplos de cálculo
¿Cómo usar la calculadora de fuerza neta?
Para calcular la fuerza neta, primero debe identificar todos los vectores de fuerza individuales que actúan sobre el objeto, a menudo representados en un diagrama de cuerpo libre (DCL). Ingrese la magnitud de cada fuerza en Newtons ($N$) y su ángulo en grados. Para mayor precisión, los ángulos deben medirse en sentido antihorario desde el eje x positivo ($0^\circ$ para la derecha, $90^\circ$ para arriba). Nuestra calculadora le permite agregar múltiples fuerzas concurrentes. Una vez que haga clic en "Calcular", la herramienta realiza la resolución trigonométrica para proporcionar los componentes horizontales ($F_x$) y verticales ($F_y$) totales, la magnitud final de la fuerza neta y la dirección resultante. Esta herramienta es esencial para resolver problemas de estática y dinámica donde se requiere determinar si un objeto está en equilibrio o acelerando.
La física de la fuerza neta: ecuaciones y definición
En física, la definición de fuerza neta es el vector único que representa la suma de todas las fuerzas que actúan sobre un cuerpo. Según la Segunda Ley de Newton ($F = ma$), la fuerza neta es directamente responsable de la aceleración de un objeto. El cálculo sigue el método de componentes de la suma de vectores: 1. Resolver cada fuerza: $F_x = F \cos(\theta)$ y $F_y = F \sin(\theta)$. 2. Sumar los componentes: $\sum F_x = F_{1x} + F_{2x} + ...$ y $\sum F_y = F_{1y} + F_{2y} + ...$. 3. Aplicar la fórmula de la fuerza resultante: $F_{net} = \sqrt{(\sum F_x)^2 + (\sum F_y)^2}$. 4. Determinar la dirección: $\theta = \tan^{-1}(\sum F_y / \sum F_x)$. Este marco matemático garantiza una alta precisión para sistemas de fuerzas en 2D, ya sean fuerzas colineales, perpendiculares o en ángulos arbitrarios.
Guía de Uso y Consejos 💡
- Si una fuerza apunta a la izquierda, use $180^\circ$; si apunta hacia abajo, use $270^\circ$.
- Recuerde que la fuerza neta es una cantidad vectorial; la magnitud por sí sola no describe el movimiento.
- Asegúrese de que todas las fuerzas estén en las mismas unidades (Newtons, Kilonewtons o Libras) antes del cálculo.
📋Pasos para Calcular
-
Enumere todas las fuerzas que actúan sobre el objeto (use un diagrama de cuerpo libre para mayor claridad).
-
Ingrese la magnitud y el ángulo de cada vector de fuerza individual.
-
Presione "Calcular" para ver la magnitud resultante, el ángulo y los componentes.
Errores a evitar ⚠️
- Tratar las fuerzas como escalares independientemente de la dirección.
- Colocación incorrecta del cuadrante para el ángulo resultante (no usar la función atan2).
- Olvidar incluir fuerzas de fricción o fuerzas normales en la suma total.
- Mezclar grados y radianes en comprobaciones trigonométricas manuales.
Aplicaciones prácticas e ingeniería📊
Cálculo de la aceleración en dinámica usando $a = F_{net} / m$.
Ingeniería estructural: Asegurar que la fuerza neta en un puente o unión de edificio sea cero (Equilibrio estático).
Aerodinámica: Sumar sustentación, peso, empuje y arrastre para determinar el rendimiento de una aeronave.
Robótica: Determinar los requisitos de par motor basados en el análisis de fuerza neta.