Net Force Calculator

Determine the vector sum of all forces acting on an object.

Resultant Force

Horizontal component (Fx): –
Vertical component (Fy): –
Magnitude (F): –
Direction (θ): –

Was this calculator helpful?

★ ★ ★ ★ ★
4.7/5 (21 votes)

Calculation Examples

Calculation Case Result
Two forces: $10 \text{ N}$ at $0^\circ$ and $10 \text{ N}$ at $180^\circ$ (Opposite directions) $F_{net} = 0 \text{ N}$ (Equilibrium)
Perpendicular forces: $3 \text{ N}$ North ($90^\circ$) and $4 \text{ N}$ East ($0^\circ$) $F_{net} = 5 \text{ N}, \theta \approx 36.87^\circ$
Tug-of-war: $50 \text{ N}$ at $30^\circ$ and $80 \text{ N}$ at $120^\circ$ $F_{net} \approx 94.3 \text{ N}, \theta \approx 89.1^\circ$

How to Use the Net Force Calculator?

To calculate net force, you must first identify all individual force vectors acting on the object, often represented in a free body diagram (FBD). Input the magnitude of each force in Newtons ($N$) and its angle in degrees. For accuracy, angles should be measured counterclockwise from the positive x-axis ($0^\circ$ for right, $90^\circ$ for up). Our calculator allows you to add multiple concurrent forces. Once you click "Calculate", the tool performs trigonometric resolution to provide the total horizontal ($F_x$) and vertical ($F_y$) components, the final magnitude of the net force, and the resultant direction. This tool is essential for solving statics and dynamics problems where determining whether an object is in equilibrium or accelerating is required.

The Physics of Net Force: Equations & Definition

In physics, the net force definition is the single vector that represents the sum of all forces acting on a body. According to Newton’s Second Law ($F = ma$), the net force is directly responsible for an object's acceleration. The calculation follows the component method of vector addition: 1. Resolve each force: $F_x = F \cos(\theta)$ and $F_y = F \sin(\theta)$. 2. Sum the components: $\sum F_x = F_{1x} + F_{2x} + ...$ and $\sum F_y = F_{1y} + F_{2y} + ...$. 3. Apply the resultant force formula: $F_{net} = \sqrt{(\sum F_x)^2 + (\sum F_y)^2}$. 4. Determine direction: $\theta = \tan^{-1}(\sum F_y / \sum F_x)$. This mathematical framework ensures high precision for 2D force systems, whether forces are collinear, perpendicular, or at arbitrary angles.Vector Addition and Net Force Diagram

Useful Tips 💡

  • If a force is pointing left, use $180^\circ$; if pointing down, use $270^\circ$.
  • Remember that net force is a vector quantity; magnitude alone does not describe the motion.
  • Ensure all forces are in the same units (Newtons, Kilonewtons, or Pounds) before calculation.

📋Steps to Calculate

  1. List all forces acting on the object (use a free body diagram for clarity).

  2. Enter the magnitude and angle for each individual force vector.

  3. Hit "Calculate" to see the resultant magnitude, angle, and components.

Mistakes to Avoid ⚠️

  1. Treating forces as scalars regardless of direction.
  2. Incorrect quadrant placement for the resultant angle (failing to use the $atan2$ function).
  3. Forgetting to include frictional forces or normal forces in the total sum.
  4. Mixing degrees and radians in manual trigonometric checks.

Practical Applications & Engineering📊

  1. Calculating acceleration in dynamics using $a = F_{net} / m$.

  2. Structural engineering: Ensuring the net force on a bridge or building joint is zero (Statical Equilibrium).

  3. Aerodynamics: Summing lift, weight, thrust, and drag to determine aircraft performance.

  4. Robotics: Determining motor torque requirements based on net force analysis.

Questions and Answers

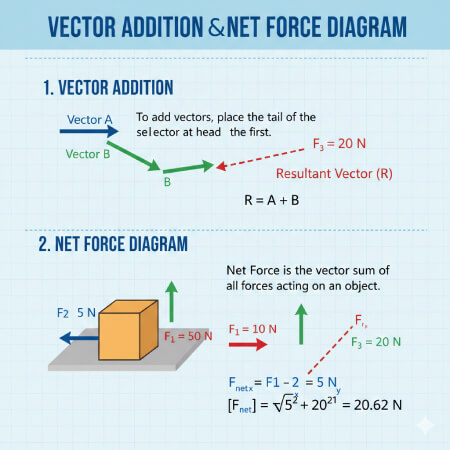
What is the Net Force and how does it determine motion?

The Net Force ($F_{net}$) is the vector sum of all individual forces acting upon a rigid body. According to Newton’s First Law, if $F_{net} = 0$, the object remains in equilibrium. If $F_{net} \neq 0$, the object must accelerate in the direction of the resultant vector, as defined by the fundamental law $F = ma$.

How do I calculate the Net Force when multiple forces act at different angles?

To find the resultant of non-collinear forces, you must perform Vector Decomposition. Each force ($F_i$) is broken into its Cartesian components: $F_x = F \cdot \cos(\theta)$ and $F_y = F \cdot \sin(\theta)$. After summing all $x$ and $y$ components, the total magnitude is found using the Pythagorean Theorem.

What is the exact formula for the magnitude of the Resultant Force?

The calculator computes the final magnitude using the resultant vector formula: $$F_{net} = \sqrt{(\sum F_x)^2 + (\sum F_y)^2}$$ This provides the absolute strength of the unbalanced force, which is then used to determine the acceleration of the mass in question.

Can a Net Force result be a negative value?

While the magnitude of a force vector is always a non-negative scalar (e.g., $10\text{ N}$), the components ($F_x, F_y$) can be negative, indicating direction relative to the coordinate axes. Our calculator provides the absolute magnitude and a 360-degree heading to define the force's direction precisely.

What happens to an object when the Net Force is exactly zero?

When $F_{net} = 0$, the object is in Static or Dynamic Equilibrium. This means there is no change in the state of motion: an object at rest stays at rest, and an object in motion continues at a constant velocity. This principle is the foundation of Statics in civil and structural engineering.

Why is a Free Body Diagram (FBD) essential for this calculation?

A Free Body Diagram is a mandatory graphical tool used to isolate an object and visualize all external force vectors (Gravity, Normal, Tension, Friction). Using an FBD ensures that no forces are omitted before inputting values into the net force calculator, preventing critical errors in Force Balance analysis.

How does this calculator determine the final direction (Angle)?

The tool calculates the resultant angle using the arctangent function: $\theta = \arctan(\sum F_y / \sum F_x)$. By analyzing the signs of the components, it correctly identifies the quadrant of the force, providing a precise heading relative to the positive x-axis ($0^\circ$ to $359^\circ$).

🔢Try More Calculators

Potential Energy Calculator
Work Calculator
Power Conversion Calculator
Disclaimer: This calculator is designed to provide helpful estimates for informational purposes. While we strive for accuracy, financial (or medical) results can vary based on local laws and individual circumstances. We recommend consulting with a professional advisor for critical decisions.