Kalkulator Gaya Netto

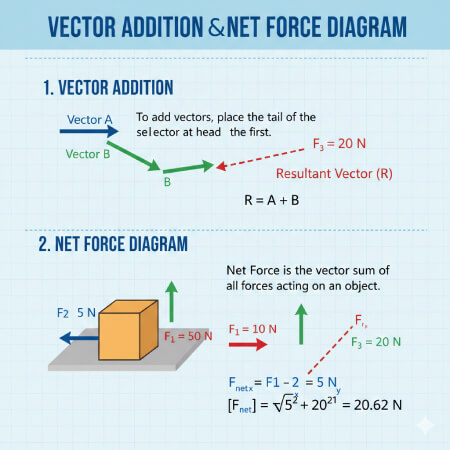
Tentukan jumlah vektor dari semua gaya yang bekerja pada suatu objek.

Gaya Resultan

Komponen horizontal (Fx): –
Komponen vertikal (Fy): –
Magnitudo (F): –
Arah (θ): –

Contoh Perhitungan

Kasus Perhitungan Hasil
Dua gaya: $10 \text{ N}$ pada $0^\circ$ dan $10 \text{ N}$ pada $180^\circ$ (Arah berlawanan) $F_{net} = 0 \text{ N}$ (Setimbang)
Gaya tegak lurus: $3 \text{ N}$ Utara ($90^\circ$) dan $4 \text{ N}$ Timur ($0^\circ$) $F_{net} = 5 \text{ N}, \theta \approx 36.87^\circ$
Tarik tambang: $50 \text{ N}$ pada $30^\circ$ dan $80 \text{ N}$ pada $120^\circ$ $F_{net} \approx 94.3 \text{ N}, \theta \approx 89.1^\circ$

Bagaimana Cara Menggunakan Kalkulator Gaya Netto?

Untuk menghitung gaya netto, Anda harus terlebih dahulu mengidentifikasi semua vektor gaya individual yang bekerja pada objek, yang sering direpresentasikan dalam diagram benda bebas (DBB). Masukkan besar setiap gaya dalam Newton ($N$) dan sudutnya dalam derajat. Untuk akurasi, sudut harus diukur berlawanan arah jarum jam dari sumbu x positif ($0^\circ$ untuk kanan, $90^\circ$ untuk atas). Kalkulator kami memungkinkan Anda menambahkan beberapa gaya konkuren. Setelah Anda mengklik "Hitung", alat ini akan melakukan resolusi trigonometri untuk memberikan total komponen horizontal ($F_x$) dan vertikal ($F_y$), besar akhir gaya netto, dan arah resultannya. Alat ini sangat penting untuk menyelesaikan masalah statika dan dinamika guna menentukan apakah suatu objek dalam keadaan setimbang atau mengalami percepatan.

Fisika Gaya Netto: Persamaan & Definisi

Dalam fisika, definisi gaya netto adalah vektor tunggal yang mewakili jumlah dari semua gaya yang bekerja pada suatu benda. Menurut Hukum Kedua Newton ($F = ma$), gaya netto bertanggung jawab langsung atas percepatan suatu objek. Penghitungan mengikuti metode komponen penjumlahan vektor: 1. Uraikan setiap gaya: $F_x = F \cos(\theta)$ dan $F_y = F \sin(\theta)$. 2. Jumlahkan komponen-komponennya: $\sum F_x = F_{1x} + F_{2x} + ...$ dan $\sum F_y = F_{1y} + F_{2y} + ...$. 3. Terapkan rumus gaya resultan: $F_{net} = \sqrt{(\sum F_x)^2 + (\sum F_y)^2}$. 4. Tentukan arah: $\theta = \tan^{-1}(\sum F_y / \sum F_x)$. Kerangka matematis ini memastikan presisi tinggi untuk sistem gaya 2D, baik gaya tersebut kolinear, tegak lurus, atau pada sudut sembarang.Diagram Penjumlahan Vektor dan Gaya Netto

Tips & Informasi 💡

  • Jika gaya mengarah ke kiri, gunakan $180^\circ$; jika mengarah ke bawah, gunakan $270^\circ$.
  • Ingatlah bahwa gaya netto adalah besaran vektor; besar saja tidak cukup untuk menggambarkan gerak.
  • Pastikan semua gaya dalam satuan yang sama (Newton, Kilonewton, atau Pound) sebelum perhitungan.

📋Langkah Menghitung

  1. Daftar semua gaya yang bekerja pada objek (gunakan diagram benda bebas agar jelas).

  2. Masukkan besar dan sudut untuk setiap vektor gaya individual.

  3. Klik "Hitung" untuk melihat besar resultan, sudut, dan komponennya.

Kesalahan yang Harus Dihindari ⚠️

  1. Memperlakukan gaya sebagai skalar tanpa memperhatikan arah.
  2. Penempatan kuadran yang salah untuk sudut resultan (gagal menggunakan fungsi atan2).
  3. Lupa memasukkan gaya gesek atau gaya normal dalam total penjumlahan.
  4. Mencampur derajat dan radian dalam pengecekan trigonometri manual.

Aplikasi Praktis & Teknik📊

  1. Menghitung percepatan dalam dinamika menggunakan $a = F_{net} / m$.

  2. Teknik struktural: Memastikan gaya netto pada jembatan atau sambungan bangunan adalah nol (Kesetimbangan Statis).

  3. Aerodinamika: Menjumlahkan gaya angkat, berat, dorong, dan hambat untuk menentukan performa pesawat.

  4. Robotika: Menentukan persyaratan torsi motor berdasarkan analisis gaya netto.

Pertanyaan Seputar Layanan Kami

Apa itu gaya netto?

Gaya netto adalah jumlah vektor dari semua gaya yang bekerja pada suatu benda. Ini mewakili total gaya tidak seimbang yang menyebabkan benda mengubah keadaan geraknya, sesuai dengan Hukum Pertama Newton.

Bagaimana cara mencari gaya netto jika banyak gaya bekerja ke arah berbeda?

Anda harus menguraikan setiap gaya ke dalam komponen horizontal (x) dan vertikal (y) menggunakan sinus dan kosinus. Jumlahkan komponen x dan y secara terpisah, lalu gunakan teorema Pythagoras untuk menemukan besar akhirnya.

Apa rumus untuk besar gaya netto?

Rumusnya adalah $F_{net} = \sqrt{(\sum F_x)^2 + (\sum F_y)^2}$, di mana $\sum F_x$ dan $\sum F_y$ adalah jumlah dari komponen-komponen vektor.

Bisakah gaya netto bernilai negatif?

Besar vektor gaya selalu berupa nilai non-negatif. Namun, komponennya ($F_x$ atau $F_y$) bisa bernilai negatif, yang menunjukkan arah di sepanjang sumbu koordinat.

Apa yang terjadi jika gaya netto adalah nol?

Ketika gaya netto nol, benda berada dalam keadaan setimbang. Benda akan tetap diam atau terus bergerak dengan kecepatan konstan dalam garis lurus.

Mengapa diagram benda bebas penting untuk gaya netto?

Diagram benda bebas adalah alat grafis yang digunakan untuk memvisualisasikan semua gaya eksternal. Ini adalah langkah penting untuk memastikan tidak ada gaya yang terlewatkan sebelum menggunakan kalkulator.

Bagaimana kalkulator ini menangani arah?

Kalkulator ini menggunakan sistem koordinat Kartesius standar. Ia menghitung sudut $\theta$ relatif terhadap sumbu x positif, memberikan arah 360 derajat yang tepat untuk vektor resultan.

🔢Rekomendasi Kalkulator Lainnya

Kalkulator Energi Potensial
Kalkulator Usaha (Work)
Kalkulator Energi Kinetik
Catatan: Kalkulator ini dirancang untuk memberikan estimasi yang bermanfaat untuk tujuan informasi. Meskipun kami mengupayakan akurasi, hasil dapat bervariasi berdasarkan hukum setempat dan keadaan individu. Kami menyarankan untuk berkonsultasi dengan penasihat profesional untuk keputusan penting.