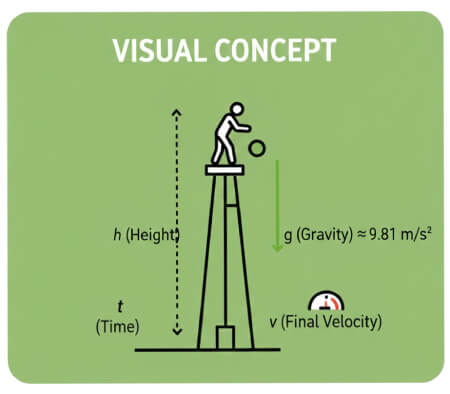
Calculateur de Chute Libre

Analysez le mouvement d'un objet tombant sous la seule influence de la gravité.

Hauteur / Distance parcourue (m): Temps de chute (s): Vitesse finale (m/s): Accélération due à la gravité g (m/s²):

Méthode de calcul (étape par étape)

Hypothèses : vitesse initiale nulle, pas de résistance de l'air. Équations cinématiques utilisées :

h = ½ g t² — hauteur / distance parcourue
v = g t — vitesse finale à l'impact
t = √(2h / g) — temps de chute
h = v² / (2g) — hauteur à partir de la vitesse
t = v / g — temps à partir de la vitesse

Accélération due à la gravité : g = 9.81 m/s²

Saisissez exactement une des valeurs : hauteur, temps ou vitesse. La valeur de g peut être ajustée ci-dessus.

Exemples de calcul

Cas de calcul	Résultat
Objet lâché du haut de la Tour Eiffel ($330 \text{ m}$)	$t \approx 8.2 \text{ s}, v \approx 80.44 \text{ m/s}$
Hauteur de chute de $150 \text{ ft}$ (Unités impériales, $g = 32.2 \text{ ft/s}^2$)	$t \approx 3.05 \text{ s}, v \approx 98.28 \text{ ft/s}$
Durée de chute de $10 \text{ secondes}$ à haute altitude	$d \approx 490.5 \text{ m}, v \approx 98.1 \text{ m/s}$

Comment utiliser le calculateur de chute libre ?

Pour utiliser le calculateur de chute libre, définissez vos variables cinématiques connues. Sélectionnez le paramètre cible : durée de la chute ($t$), vitesse d'impact finale ($v$) ou déplacement total ($d$). Saisissez les données dans les champs respectifs ; pour une chute standard au repos, assurez-vous que la vitesse initiale ($v_0$) est nulle. Choisissez votre système d'unités préféré — Métrique ($m, s$) ou Impérial ($ft, s$). L'algorithme applique l'accélération standard de la pesanteur ($g \approx 9.81 \text{ m/s}^2$ ou $32.2 \text{ ft/s}^2$). En cliquant sur "Calculer", le système exécute les équations cinématiques pour fournir des résultats instantanés, incluant les étapes intermédiaires pour une clarté pédagogique. Cet outil est optimisé pour la mécanique newtonienne où la résistance de l'air est négligeable.

Cadre Mathématique et Équations Cinématiques

La chute libre est définie comme un mouvement rectiligne à accélération constante. Dans le vide ou en ignorant la traînée aérodynamique, le mouvement est régi par les équations fondamentales suivantes : 1. Déplacement : $d = \frac{1}{2}gt^2$ | 2. Vitesse Finale : $v = gt$ | 3. Relation Vitesse-Déplacement : $v = \sqrt{2gd}$. Où $g$ représente l'intensité du champ gravitationnel local. Ces dérivations supposent que l'objet part d'un état de repos ($v_0 = 0$). Dans les milieux fluides (comme l'air), les objets atteignent finalement une vitesse terminale due aux forces de traînée, un facteur non pris en compte dans ce modèle newtonien simplifié. Dynamique de la Chute Libre

Conseils d’Experts 💡

Assurez-vous que la vitesse initiale est nulle pour les scénarios de chute pure au repos.
Utilisez des unités cohérentes dans tous les champs de saisie pour garantir l'intégrité du calcul.

📋Étapes de calcul

Sélectionnez la variable connue (hauteur, durée ou vitesse).
Spécifiez le système d'unités (Métrique ou Impérial).
Exécutez le calcul pour obtenir des données cinématiques complètes.

Erreurs à éviter ⚠️

Ignorer les effets de la résistance de l'air sur les objets ayant un rapport surface/masse élevé.
Confondre la masse et le poids ; dans le vide, tous les objets tombent à la même vitesse quelle que soit leur masse.
Mesures de temps imprécises lors d'expériences manuelles entraînant des erreurs exponentielles sur la distance.
Appliquer ces équations à des vitesses relativistes ou à des champs gravitationnels non uniformes.

Applications Pratiques📊

Calcul de l'énergie d'impact et de la vitesse pour les évaluations de sécurité structurelle.
Vérification des données expérimentales lors des séances de laboratoire de mécanique classique.
Estimation de la hauteur de structures verticales basée sur des chutes chronométrées.
Modélisation de la trajectoire initiale pour les largages de charges ou la physique des drones.

Questions Fréquentes (FAQ)

Quelle est la définition de la chute libre ?

En physique newtonienne, la chute libre est tout mouvement d'un corps où la gravité est la seule force agissant sur lui. Cela implique un environnement sous vide sans traînée aérodynamique. Dans ces conditions, l'objet subit une accélération constante de $g \approx 9.81 \text{ m/s}^2$ vers le centre de la Terre, indépendamment de sa masse ou de sa forme. Ce principe a été démontré par Galilée.

Comment calculer le temps de chute à partir d'une hauteur spécifique ?

Pour dériver la durée de la chute à partir d'un déplacement connu ($d$), nous réorganisons l'équation cinématique $d = \frac{1}{2}gt^2$. En résolvant pour $t$, nous obtenons la formule $t = \sqrt{2d/g}$. Ce calcul suppose que l'objet commence avec une vitesse initiale nulle.

Quelle est la formule de la vitesse finale ?

La vitesse juste avant l'impact est déterminée par le temps ou la distance. Si le temps est connu, nous utilisons $v = gt$. Si la distance est connue, nous utilisons l'équation de Torricelli : $v = \sqrt{2gd}$. Ces formules montrent que la vitesse augmente linéairement avec le temps.

Cet outil tient-il compte de la traînée atmosphérique ?

Non, ce calculateur est conçu pour une chute libre "idéale", en supposant le vide. Dans le monde réel, la force de traînée de l'air augmente jusqu'à égaler la force de gravité, atteignant une vitesse terminale.

La masse de l'objet est-elle requise pour le calcul ?

Non. Selon le principe d'équivalence, la masse n'affecte pas la vitesse de chute dans le vide. La masse gravitationnelle et la masse inertielle s'annulent dans l'équation du mouvement ($ma = mg$). C'est pourquoi notre calculateur ne nécessite pas de saisie de la masse.

Quelle constante est utilisée pour la gravité ?

Le calculateur utilise l'accélération standard due à la pesanteur définie par la CGPM, soit $g_n = 9.80665 \text{ m/s}^2$ pour les calculs métriques et environ $32.174 \text{ ft/s}^2$ pour le système impérial.

Note : Ce calculateur est conçu pour fournir des estimations utiles à des fins d'information. Bien que nous fassions tout notre possible pour garantir l'exactitude, les résultats peuvent varier en fonction des lois locales et des circonstances individuelles. Nous vous recommandons de consulter un conseiller professionnel pour toute décision importante.