Kalkulator Gerak Jatuh Bebas

Analisis gerak benda yang jatuh di bawah pengaruh gravitasi saja. Hitung kecepatan, waktu, dan jarak dengan presisi tinggi.

Ketinggian / Jarak jatuh (m): Waktu jatuh (s): Kecepatan akhir (m/s): Percepatan gravitasi g (m/s²):

Metode perhitungan (langkah demi langkah)

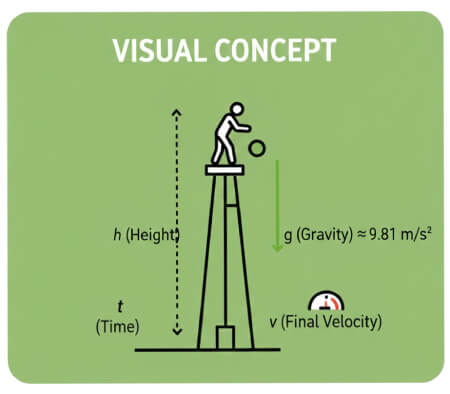
Asumsi: kecepatan awal nol, tanpa hambatan udara. Persamaan kinematika yang digunakan:

h = ½ g t² — ketinggian / jarak jatuh
v = g t — kecepatan akhir saat tumbukan
t = √(2h / g) — waktu jatuh
h = v² / (2g) — ketinggian dari kecepatan
t = v / g — waktu dari kecepatan

Percepatan gravitasi: g = 9.81 m/s²

Masukkan tepat satu dari: ketinggian, waktu atau kecepatan. Nilai g dapat disesuaikan di atas.

Contoh Perhitungan

Kasus Perhitungan	Hasil
Benda dijatuhkan dari puncak Monas ($132 \text{ m}$)	$t \approx 5.19 \text{ s}, v \approx 50.9 \text{ m/s}$
Ketinggian pelepasan $150 \text{ kaki}$ (satuan Imperial, $g = 32.2 \text{ ft/s}^2$)	$t \approx 3.05 \text{ s}, v \approx 98.28 \text{ ft/s}$
Durasi jatuh $10 \text{ detik}$ dari ketinggian tinggi	$d \approx 490.5 \text{ m}, v \approx 98.1 \text{ m/s}$

Bagaimana cara menggunakan Kalkulator Jatuh Bebas?

Pilih parameter target: durasi jatuh ($t$), kecepatan impak akhir ($v$), atau total jarak ($d$). Masukkan data ke kolom yang tersedia; untuk jatuhan standar dari posisi diam, pastikan kecepatan awal ($v_0$) adalah nol. Pilih sistem koordinat yang Anda inginkan—Metrik ($m, s$) atau Imperial ($ft, s$). Algoritma menerapkan percepatan gravitasi standar ($g \approx 9.81 \text{ m/s}^2$ atau $32.2 \text{ ft/s}^2$). Setelah mengklik "Hitung", sistem menjalankan persamaan kinematika untuk memberikan hasil instan, termasuk langkah-langkah menengah untuk kejelasan pedagogis. Alat ini dioptimalkan untuk mekanika Newton di mana hambatan udara dianggap abaikan, menjadikannya ideal untuk demonstrasi pendidikan, perkiraan teknik, dan pemecahan masalah fisika.

Kerangka Matematika & Persamaan Kinematika

Jatuh bebas didefinisikan sebagai gerak lurus dengan percepatan konstan. Dalam ruang hampa atau mengabaikan hambatan udara, gerak diatur oleh persamaan fundamental berikut: 1. Jarak: $d = \frac{1}{2}gt^2$ | 2. Kecepatan Akhir: $v = gt$ | 3. Relasi Kecepatan-Jarak: $v = \sqrt{2gd}$. Di mana $g$ mewakili kekuatan medan gravitasi lokal. Penurunan ini mengasumsikan benda mulai dari keadaan diam ($v_0 = 0$) dan mengalami medan gravitasi yang seragam. Dalam medium fluida (seperti udara), benda akhirnya mencapai kecepatan terminal karena gaya hambat, faktor yang tidak diperhitungkan dalam model Newtonian sederhana ini. Dinamika Jatuh Bebas

Tips & Informasi 💡

Pastikan kecepatan awal diatur ke nol untuk skenario jatuh bebas murni dari keadaan diam.
Gunakan satuan yang konsisten di semua bidang input untuk menjaga integritas perhitungan.

📋Langkah Menghitung

Pilih variabel yang diketahui (tinggi, durasi, atau kecepatan).
Tentukan sistem satuan (Metrik atau Imperial).
Klik "Hitung" untuk mendapatkan data kinematika yang komprehensif.

Kesalahan yang Harus Dihindari ⚠️

Mengabaikan efek hambatan udara pada benda dengan rasio luas permukaan terhadap massa yang tinggi.
Membingungkan massa dengan berat; di ruang hampa, semua benda jatuh dengan laju yang sama tanpa memandang massa.
Pengukuran waktu yang tidak akurat dalam eksperimen manual yang menyebabkan kesalahan eksponensial dalam jarak.
Menerapkan persamaan ini pada kecepatan relativistik atau medan gravitasi yang tidak seragam.

Aplikasi Praktis📊

Menghitung energi impak dan kecepatan untuk penilaian keselamatan struktural.
Verifikasi data eksperimen dalam sesi laboratorium mekanika klasik.
Estimasi tinggi struktur vertikal berdasarkan waktu jatuh yang diukur.
Pemodelan lintasan awal untuk peluncuran muatan atau fisika drone.

Pertanyaan Seputar Layanan Kami

Apa yang dimaksud dengan jatuh bebas?

Dalam fisika Newton, jatuh bebas adalah gerak benda di mana gravitasi adalah satu-satunya gaya yang bekerja padanya. Ini menyiratkan lingkungan hampa udara di mana tidak ada hambatan aerodinamis atau gaya apung. Dalam kondisi ini, benda mengalami percepatan konstan $g \approx 9.81 \text{ m/s}^2$ menuju pusat Bumi, tanpa memandang massa, komposisi, atau bentuknya. Prinsip ini terkenal didemonstrasikan oleh Galileo Galilei.

Bagaimana cara menghitung waktu jatuh dari ketinggian tertentu?

Untuk mencari durasi jatuh dari jarak ($d$) yang diketahui, kita mengatur ulang persamaan kinematika $d = \frac{1}{2}gt^2$. Menyelesaikan untuk $t$ memberikan rumus $t = \sqrt{2d/g}$. Perhitungan ini mengasumsikan benda mulai dengan kecepatan awal nol. Misalnya, jatuh dari $100$ meter di Bumi akan memakan waktu sekitar $\sqrt{200 / 9.81} \approx 4.52$ detik.

Apa rumus untuk kecepatan akhir?

Kecepatan tepat sebelum benturan ditentukan oleh waktu atau jarak. Jika waktu diketahui, kita menggunakan $v = gt$. Jika jarak diketahui, kita menggunakan persamaan Torricelli: $v = \sqrt{2gd}$. Rumus-rumus ini menunjukkan bahwa kecepatan meningkat secara linier dengan waktu tetapi mengikuti hubungan akar kuadrat dengan ketinggian jatuh.

Apakah alat ini memperhitungkan hambatan udara?

Tidak, kalkulator khusus ini dirancang untuk jatuh bebas "ideal", dengan asumsi ruang hampa atau hambatan udara yang dapat diabaikan. Dalam skenario dunia nyata, saat benda dipercepat, gaya hambat udara meningkat hingga sama dengan gaya gravitasi ke bawah, mencapai kecepatan terminal.

Apakah massa benda diperlukan untuk perhitungan?

Salah satu aspek mekanika klasik yang paling berlawanan dengan intuisi adalah bahwa massa tidak mempengaruhi laju jatuh di ruang hampa. Menurut prinsip ekivalensi, massa gravitasi dan massa inersia saling meniadakan dalam persamaan gerak ($ma = mg$). Karena itu, kalkulator kami tidak memerlukan input massa.

Konstanta apa yang digunakan untuk gravitasi?

Kalkulator menggunakan percepatan standar akibat gravitasi yang ditetapkan oleh CGPM, yaitu $g_n = 9.80665 \text{ m/s}^2$ untuk perhitungan metrik. Untuk pengguna yang memilih sistem Imperial, nilainya kira-kira $32.174 \text{ ft/s}^2$.

Catatan: Kalkulator ini dirancang untuk memberikan estimasi yang bermanfaat untuk tujuan informasi. Meskipun kami mengupayakan akurasi, hasil dapat bervariasi berdasarkan hukum setempat dan keadaan individu. Kami menyarankan untuk berkonsultasi dengan penasihat profesional untuk keputusan penting.