Simple Pendulum Calculator
Compute Pendulum Period, Length, and Frequency Instantly
Please provide exactly two of the four fields.
📋How to Use the Simple Pendulum Calculator?
-
Enter the pendulum length, period, or frequency into the area specified.
-
Select the units (meters for length, seconds for dropping time, hertz for frequency).
-
Click on the "Calculate" to show the result and information about the motion.
To analyze a pendulum, enter one known value: the length of the string, the period of one full swing, or the frequency of oscillations. Ensure you select the correct units, such as meters for length or seconds for the period.
Click "Calculate" to find the remaining variables. This tool assumes a "simple" pendulum, meaning the mass of the string is negligible and the swing angle is small. This is an essential resource for physics students and educators studying simple harmonic motion and gravity.
Useful Tips💡
-
Measure the length from the pivot point to the center of mass of the pendulum bob.
-
Keep the swing angle small (under 15 degrees) for the most accurate results using these formulas.
Mistakes to Avoid ⚠️
- Thinking mass affects the period: In a simple pendulum, the weight of the bob does not change the time of the swing.
- Measuring to the top of the bob: You must measure to the center of the mass (usually the middle of the bob).
- Large angles: If the pendulum swings too wide, the standard formula becomes less accurate.
How Calculations Are Performed
The simple pendulum calculator uses T = 2π√(L/g), where T is the period, L is the length, and g is the gravitational acceleration (9.81 m/s²) . This formula is verified by the International System of Units (SI) for standard conditions. The calculator calculates frequency as f = 1/T. The tool also solves for the unknown variable based on user input; knowing that even for small swings it gives consistent and dependable results. 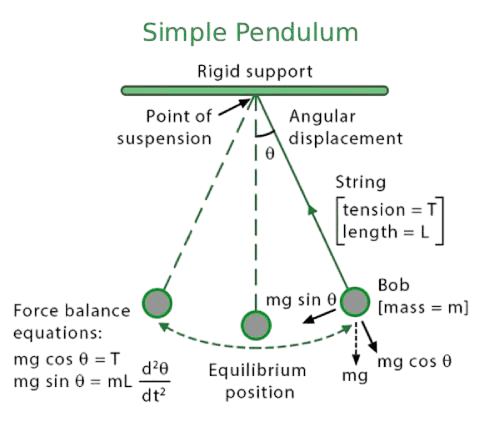
Practical Applications📊
-
Provide students with a hands-on interaction to understand the physics concepts of pendulum motion
-
Assist as you set up experiments with applicable distance measurements.
-
Help with the observations associated with pendulum based clocks or timing devices.
Questions and Answers
What is a simple pendulum calculator?
A pendulum calculator is an online tool that calculates the basic parameters of a simple pendulum, including the period, length, and frequency based on information supplied by the user. The oscillator calculator takes the complexity out of physics calculations, and in addition to its usefulness to students studying oscillation dynamics, it is useful for educators and researchers studying pendulum mechanisms.
How to calculate the period of a pendulum?
To calculate the period of a pendulum, in the our tool, simply input the Swing’s length in meters and then select "Calculate." The calc will substitute into the period calculation and output the value. For example, if a user wants to find the period of a 1.00-m-long pendulum, the tool will calculate this period as T ≈ 2.01 seconds.
What is the frequency of a pendulum?
In the case of a pendulum, a it’s frequency is the number of oscillations per second (Hertz, or Hz). Frequency is calculated by taking the inverse of the period, as follows f = 1/T; remember the pendulum period from above is based on T = 2π √(L/g). For example, if a pendulum oscillates every 2 seconds, then: f = 1/T therefore the frequency is 0.5 Hz. If you enter the length or period into the Pendulum Calculator, it will calculate the frequency in no time! This can help when looking at the analysis of, say, pendulum motion in the context of a physics experiment or timekeeping object, while incorporating the notion of oscillations and dynamics of the pendulum that is stylized in the unit of Hertz (Hz).
How does pendulum length affect the period?
The period of a pendulum has a length dependent relationship as referenced in the equation T = 2π√(L/g). Longer Swings have longer periods, and they take longer to complete one oscillation, thus having a higher period. A Swing with a length of .5 m has a shorter period than the period of the one with a length of 1 m, if both pendulum in are in standard gravity.
How to analyze a pendulum in swing?
Analyzing a pendulum in swing involves studying its period, frequency, and amplitude during oscillation. Using the Swing Calculator, input the length to calculate the period (T = 2π√(L/g)) or frequency (f = 1/T). For example, a 0.79-m pendulum has a period of about 1.78 seconds. Amplitude, the maximum angle of swing, affects motion minimally at small angles (less than 15°). For precise analysis, measure length accurately and ensure small-angle oscillations. This tool helps explore pendulum swing dynamics for experiments or clock design, but for large amplitudes or velocity analysis, consult advanced physics resources.


