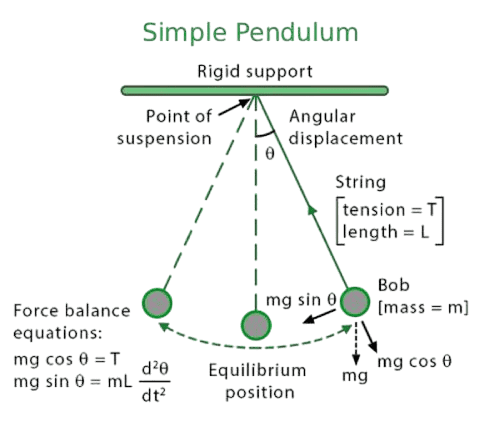
Calculadora de Pêndulo

Calcule período, comprimento ou frequência de um pêndulo simples online.

Por favor, forneça exatamente dois dos quatro campos.

Exemplos de Cálculo

Caso de Cálculo Resultado
Comprimento 1 metro na Terra Período: ~2,01 segundos
Comprimento 0,25 metros Período: ~1,00 segundo
Pêndulo na Lua (g=1,62) Período mais lento que na Terra

Como Usar a Calculadora de Pêndulo Simples?

Para calcular propriedades de um oscilador utilizando nosso instrumento, insira o valor da propriedade conhecida (comprimento, período, frequência) em seu campo associado. Selecione o comprimento em metros, o período em segundos e a frequência em hertz. Clique em "Calcular" para ver os resultados. Nossa ferramenta usa a fórmula básica para um pêndulo simples, assumindo (1) ângulos de oscilação pequenos e (2) aceleração gravitacional constante (9.81 m/s²). Os resultados são fornecidos imediatamente e mostrarão o período, comprimento ou frequência junto com um breve fundo sobre o movimento harmônico do pêndulo. Este é um ótimo calculador para estudantes, professores e entusiastas da física estudando a dinâmica de oscilações. Certifique-se de usar entradas corretas e unidades consistentes para dados confiáveis.

Como São Realizados os Cálculos

A calculadora de pêndulo simples usa T = 2π√(L/g), onde T é o período, L é o comprimento e g é a aceleração gravitacional (9.81 m/s²). Esta fórmula está verificada pelo Sistema Internacional de Unidades (SI) para condições padrão. O instrumento calcula a frequência como f = 1/T. A ferramenta também resolve a variável desconhecida baseada na entrada do usuário; sabendo que mesmo para balanços pequenos dá resultados consistentes e confiáveis. Pêndulo Simples

Dicas Úteis 💡

  • Faça ângulos de pêndulo pequenos (<15°) para que a fórmula funcione corretamente.
  • Realize medições de comprimento desde o pivô ao centro de massa para dados mais confiáveis.

📋Passos para Calcular

  1. Insira o comprimento do pêndulo, período ou frequência na área especificada.

  2. Selecione as unidades (metros para comprimento, segundos para tempo de queda, hertz para frequência).

  3. Clique em "Calcular" para mostrar o resultado e informação sobre o movimento harmônico.

Erros a evitar ⚠️

  1. Incluir a massa do objeto na fórmula (o período não depende da massa).
  2. Não converter o comprimento do fio para metros antes de usar a gravidade.
  3. Usar ângulos de oscilação muito grandes (a fórmula padrão é para ângulos pequenos).
  4. Utilizar o valor padrão de gravidade (9,8) em locais com variações geográficas.

Aplicações Práticas📊

  1. Fornece a estudantes interação prática para entender conceitos físicos de movimento oscilatório.

  2. Assiste na configuração de experimentos com medições de distância aplicáveis.

  3. Ajuda com observações associadas a relógios baseados em pêndulos ou dispositivos de temporização.

Perguntas e Respostas

O que é uma calculadora de pêndulo simples?

Uma Calculadora de Pêndulo Simples é uma ferramenta online que calcula parâmetros básicos de um pêndulo simples, incluindo período, comprimento e frequência baseada em informação fornecida pelo usuário. O calculador de oscilador elimina a complexidade de cálculos físicos, e além de sua utilidade para estudantes estudando dinâmica de oscilações, é útil para educadores e pesquisadores analisando mecanismos de pêndulos.

Como calcular o período de um pêndulo?

Para calcular o período de um pêndulo, em nossa ferramenta, simplesmente insira o comprimento do balanço em metros e selecione "Calcular." O instrumento substituirá no cálculo do período e output o valor. Por exemplo, se um usuário quiser encontrar o período de um pêndulo de 1.00 m de comprimento, a ferramenta calculará este período como T ≈ 2.01 segundos.

Qual é a frequência de um pêndulo?

No caso de um pêndulo, sua frequência é o número de oscilações por segundo (Hertz, ou Hz). A frequência é calculada tomando o inverso do período, como f = 1/T; lembre-se que o período do pêndulo acima se baseia em T = 2π √(L/g). Por exemplo, se um pêndulo oscila a cada 2 segundos, então: f = 1/T portanto a frequência é 0.5 Hz. Se você inserir o comprimento ou período na Calculadora de Pêndulo, calculará a frequência em pouco tempo! Isso pode ajudar ao analisar, digamos, movimento de pêndulo no contexto de um experimento físico ou objeto de cronometragem, incorporando a noção de oscilações e dinâmica do pêndulo estilizado na unidade de Hertz (Hz).

Como o comprimento do pêndulo afeta o período?

O período de um pêndulo tem uma relação dependente do comprimento como referenciado na equação T = 2π√(L/g). Balanços mais longos têm períodos mais longos, e demoram mais para completar uma oscilação, tendo assim um período maior. Um balanço com comprimento de 0.5 m tem um período mais curto que o de um com comprimento de 1 m, se ambos estiverem em gravidade padrão.

Como analisar um pêndulo em balanço?

Analisar um pêndulo em balanço envolve estudar seu período, frequência e amplitude durante a oscilação. Usando a Calculadora de Balanço, insira o comprimento para calcular o período (T = 2π√(L/g)) ou frequência (f = 1/T). Por exemplo, um pêndulo de 0.79 m tem um período de aproximadamente 1.78 segundos. A amplitude, o ângulo máximo de balanço, afeta o movimento minimamente em ângulos pequenos (menos de 15°). Para análise precisa, meça o comprimento com exatidão e assegure oscilações de ângulo pequeno. Esta ferramenta ajuda a explorar dinâmica de balanço de pêndulo para experimentos ou design de relógios, mas para amplitudes grandes ou análise de velocidade, consulte recursos físicos avançados.

🔢Experimente Mais Calculadoras

Calculadora de Força
Calculadora de Pressão
Calculadora de Força de Atrito
Nota: Esta calculadora foi projetada para fornecer estimativas úteis para fins informativos. Embora nos esforcemos pela precisão, os resultados podem variar com base nas leis locais e circunstâncias individuais. Recomendamos consultar um consultor profissional para decisões críticas.