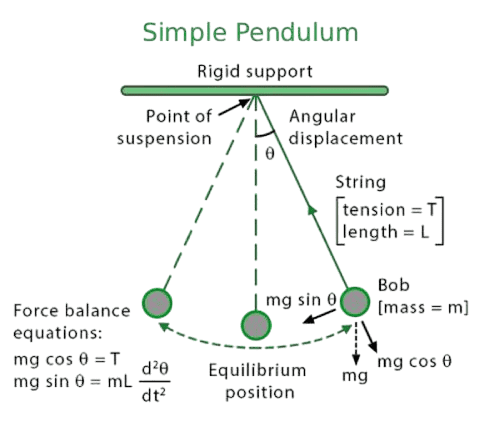
Kalkulator Bandul Sederhana

Hitung Periode, Panjang, dan Frekuensi Pendulum Secara Online.

Harap masukkan tepat dua dari empat kolom.

Contoh Perhitungan

Kasus Perhitungan Hasil
Bandul dengan panjang tali 1 meter di Bumi (g=9,8 m/s²) Periode: ~2 detik
Mencari frekuensi ayunan per menit Analisis gerak harmonik sederhana
Pengaruh gravitasi terhadap waktu ayun bandul Eksperimen gravitasi planet

Bagaimana Cara Menggunakan Kalkulator Bandul Sederhana?

Untuk menghitung properti osilator menggunakan instrumen kami, masukkan nilai yang Anda ketahui (panjang, periode, atau frekuensi) pada kolom yang tersedia. Pilih satuan panjang dalam meter, periode dalam detik, dan frekuensi dalam Hertz (Hz). Klik "Hitung" untuk melihat hasil lengkapnya. Alat ini menggunakan asumsi standar fisika yaitu sudut osilasi kecil (kurang dari 15 derajat) dan percepatan gravitasi bumi konstan sebesar 9.81 m/s2. Hasil yang muncul akan mencakup analisis gerak harmonik sederhana yang sangat berguna bagi siswa, guru, dan peneliti di Indonesia dalam melakukan praktikum fisika dasar.

Bagaimana Perhitungan Dilakukan

Kalkulator pendulum sederhana menggunakan T = 2π√(L/g), di mana T adalah periode, L adalah panjang, dan g adalah percepatan gravitasi (9.81 m/s²). Rumus ini diverifikasi oleh Sistem Internasional Satuan (SI) untuk kondisi standar. Instrumen menghitung frekuensi sebagai f = 1/T. Alat juga menyelesaikan variabel tidak diketahui berdasarkan input pengguna; mengetahui bahwa bahkan untuk ayunan kecil memberikan hasil yang konsisten dan andal. Pendulum Sederhana

Tips & Informasi 💡

  • Buat sudut pendulum kecil (<15°) agar rumus bekerja dengan benar.
  • Lakukan pengukuran panjang dari poros ke pusat massa untuk data lebih andal.

📋Langkah Menghitung

  1. Masukkan panjang pendulum, periode atau frekuensi di area yang ditentukan.

  2. Pilih unit (meter untuk panjang, detik untuk waktu jatuh, hertz untuk frekuensi).

  3. Klik "Hitung" untuk menampilkan hasil dan informasi tentang gerak harmonik.

Kesalahan yang Harus Dihindari ⚠️

  1. Menggunakan massa beban dalam rumus (padahal periode tidak tergantung massa).
  2. Lupa mengonversi panjang tali ke satuan meter sebelum menghitung.
  3. Menggunakan sudut simpangan yang terlalu besar (rumus standar hanya untuk sudut kecil).
  4. Salah memasukkan nilai gravitasi (g) yang berbeda di tempat tertentu.

Aplikasi Praktis📊

  1. Edukasi: Membantu siswa memahami konsep Gerak Harmonik Sederhana (GHS).

  2. Eksperimen: Menghitung percepatan gravitasi lokal di berbagai wilayah di Indonesia.

  3. Horologi: Dasar mekanis untuk pengaturan waktu pada jam bandul antik.

Pertanyaan Seputar Layanan Kami

Apa itu Kalkulator Bandul Sederhana?

Kalkulator Bandul Sederhana adalah alat online yang menghitung parameter dasar dari pendulum sederhana, termasuk periode, panjang, dan frekuensi berdasarkan informasi yang diberikan pengguna. Kalkulator osilator menghilangkan kompleksitas perhitungan fisika, dan selain kegunaannya bagi siswa yang mempelajari dinamika osilasi, berguna untuk pendidik dan peneliti yang menganalisis mekanisme pendulum.

Bagaimana menghitung periode pendulum?

Untuk menghitung periode pendulum, di alat kami, cukup masukkan panjang ayunan dalam meter dan pilih "Hitung." Instrumen akan menggantikan dalam perhitungan periode dan output nilai. Misalnya, jika pengguna ingin menemukan periode pendulum sepanjang 1.00 m, alat akan menghitung periode ini sebagai T ≈ 2.01 detik.

Apa frekuensi pendulum?

Dalam kasus pendulum, frekuensinya adalah jumlah osilasi per detik (Hertz, atau Hz). Frekuensi dihitung dengan mengambil invers dari periode, sebagai f = 1/T; ingat periode pendulum di atas berdasarkan T = 2π √(L/g). Misalnya, jika pendulum berosilasi setiap 2 detik, maka: f = 1/T sehingga frekuensi adalah 0.5 Hz. Jika Anda memasukkan panjang atau periode ke Kalkulator Bandul Sederhana, akan menghitung frekuensi dalam waktu singkat! Ini dapat membantu saat menganalisis, katakanlah, gerak pendulum dalam konteks eksperimen fisika atau objek pengatur waktu, menggabungkan gagasan osilasi dan dinamika pendulum yang distilisasi dalam unit Hertz (Hz).

Bagaimana panjang pendulum memengaruhi periode?

Periode pendulum memiliki hubungan tergantung panjang seperti yang dirujuk dalam persamaan T = 2π√(L/g). Ayunan lebih panjang memiliki periode lebih panjang, dan memakan waktu lebih lama untuk menyelesaikan satu osilasi, sehingga memiliki periode lebih besar. Ayunan dengan panjang 0.5 m memiliki periode lebih pendek daripada yang dengan panjang 1 m, jika keduanya berada di gravitasi standar.

Apa itu periode dalam pendulum?

Periode adalah waktu yang dibutuhkan oleh bandul untuk melakukan satu kali getaran penuh (kembali ke titik awal).

Bagaimana gravitasi memengaruhi bandul?

Semakin besar gravitasi, semakin cepat bandul berayun (periode lebih pendek). Di planet dengan gravitasi rendah, bandul akan berayun lebih lambat.

Apakah berat beban memengaruhi periode?

Dalam kondisi ideal (pendulum sederhana), massa atau berat beban tidak memengaruhi periode ayunan; hanya panjang tali dan gravitasi yang berpengaruh.

🔢Rekomendasi Kalkulator Lainnya

Kalkulator Gaya
Kalkulator Tekanan
Kalkulator Gaya Gesek
Catatan: Kalkulator ini dirancang untuk memberikan estimasi yang bermanfaat untuk tujuan informasi. Meskipun kami mengupayakan akurasi, hasil dapat bervariasi berdasarkan hukum setempat dan keadaan individu. Kami menyarankan untuk berkonsultasi dengan penasihat profesional untuk keputusan penting.