Half-Life Calculator
Calculate radioactive disintegration in seconds.
Please enter the required details and click Calculate.
📋How to Use Half Life Calculator?
-
Enter the initial amount and half-life of the object.
-
Enter elapsed time and proper unit(s).
-
Click "Calculate" to view the remaining amount and decay details.
Input the starting quantity of the substance, the elapsed time and the decay interval value into the half-life estimator. Make sure to choose the correct units for the quantity and elapsed time (i.e., grams, years, days) before you press the "Calculate" button.
After your click, the estimator will quickly show you how much is remaining, or the number of half-lives that have elapsed. The estimator will provide very quick output providing the decay constant, the percentage of the original quantity that remains, etc.
An example estimated half-lives with a starting amount of 100g, half-life of 8 days and elapsed time of 16 days would yield 25g remaining, because 100 g decayed 1/2 to 50g (the first half = 8 days), then into 27.5g (second half = 8 days decay).
Useful Tips💡
-
Input initial quantity and time period accurately.
-
Use reliable decomposition constant for precise results.
How Are Half-Life Calculations Performed?
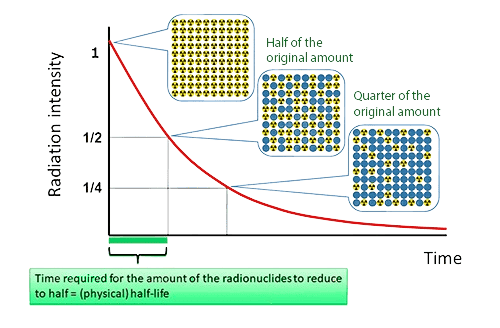
Half-life calculations follow a generic form for the exponential decay of the amount of a substance remaining, which is verified by the International non-invasive evidence and monitoring entityAtomic Energy Agency (IAEA) to be A = A₀ * (1/2)^(t/T), where A is the amount remaining, A₀ is the original amount, t is the amount of time elapsed, and T is the half-life. The disintegration constant, λ, can alternatively be calculated using the equation λ = ln(2)/T. These equations can model radioactive decay and work for many isotope types.
Practical Applications📊
-
Monitoring radioactive decay for nuclear application or medical applications.
-
Estimating remaining concentration of drug for pharmacokinetics studies.
-
Determining the age of fossils using carbon-14 dating, which requires knowledge of half-life.
Questions and Answers
What is a half-life calculator?
A half-life calculator is an online tool that calc the amount of time it takes an object or substance to reduce to half of its original amount due to radioactive decay. You enter the initial amount of your object, the Decay interval of the object and the calculator will calculate the remaining amounts based on the half-life you provided.
How to calculate half-life of an isotope?
To find out the Decay interval of an isotope, you need to enter the initial amount, final amount and elapsed time into the half-life calculator. This will enable the calculator to use its exponential decay formula to estimate the decay period era.
What is the half-life formula?
The half-life formula is an equation to determine decomposition rates for radioactive substances: A=A0(1/2)t/T, where A is the amount remaining, A0 is the initial amount, t is elapsed time and T is half-life. It is used to simulate exponential decomposition in chemistry and physics. This formula is supported and used by the IAEA as the most accurate way to calculate disintegration for isotopes such as carbon-14 or iodine-131.
How to find half-life from decay rate?
The decomposition constant (λ) is related to the half-life (T) by T = ln(2)/λ. You can simply plug the constant into a calculator and estimate the decay period, while ensuring that you are using accurate units in order to get a good result.
What is radioactive decay?
Radioactive decay describes the process that occurs when unstable isotopes expel energy as radiation and diminish or decomposition in their quantity over a period of time. A half-life calculator is a way to estimate this decay using various substances.
How to use a half-life estimator for drugs?
For calculating Decay interval related to drug administration, all you need to do is enter your initial dose, the elapsed time, and the Decay interval period into the calculator, and it will estimate the concentration of the drug remaining in order to assist you when using dose planning software such as CalcMate.