Calculadora de Fuerza de Fricción
Calcule la fricción usando el coeficiente y la fuerza normal.
Pasos del cálculo
Ejemplos de cálculo
¿Cómo usar la calculadora de fuerza de fricción?
Esta herramienta está diseñada para resolver problemas de mecánica que involucran fricción. Primero, seleccione el tipo de fricción: estática (para objetos en reposo) o cinética (para objetos en deslizamiento), ya que sus coeficientes difieren. Ingrese el coeficiente de fricción ($\mu$), que representa la interacción entre los dos materiales. Luego, proporcione la fuerza normal ($N$) en Newtons. Si la fuerza normal es desconocida, puede ingresar la masa del objeto ($m$) y el ángulo de inclinación ($\theta$).
Para superficies horizontales, la fuerza normal es simplemente $N = m \cdot g$. En un plano inclinado, se reduce a $N = m \cdot g \cdot \cos(\theta)$. La calculadora calcula automáticamente estos valores y compara la fricción contra la componente gravitacional $m \cdot g \cdot \sin(\theta)$ para predecir si ocurrirá un deslizamiento. Este enfoque sigue las leyes de Newton y es estándar para tareas de ingeniería y física.
La Física de la Fricción: Fórmulas y Principios
El cálculo de la fricción seca se rige por las leyes de Amontons-Coulomb. La relación principal se define por la fórmula $F_f = \mu \cdot N$, donde $F_f$ es la fuerza de fricción, $\mu$ es el coeficiente y $N$ es la fuerza normal. Fricción Estática ($F_s$): Actúa como una fuerza autoajustable que iguala la fuerza aplicada hasta un umbral máximo $F_{s, max} = \mu_s \cdot N$. Si la fuerza paralela excede este valor, comienza el movimiento. Fricción Cinética ($F_k$): Una vez que el objeto se desliza, la fuerza de fricción generalmente cae a un valor constante $F_k = \mu_k \cdot N$. En la mayoría de los sistemas físicos, $\mu_s > \mu_k$, lo que explica por qué se requiere más fuerza para iniciar el movimiento de un objeto que para mantenerlo deslizándose. En inclinaciones, la fuerza normal se modifica por el coseno del ángulo, lo que hace que la fricción sea menor a medida que la pendiente se vuelve más pronunciada.
Guía de Uso y Consejos 💡
- El coeficiente $\mu$ depende de ambos materiales en contacto (por ejemplo, caucho sobre asfalto seco frente a caucho sobre hielo húmedo).
- Siempre use el coeficiente estático para verificar el inicio del movimiento.
- Verifique que el ángulo se mida desde el plano horizontal para obtener resultados correctos.
📋Pasos para Calcular
-
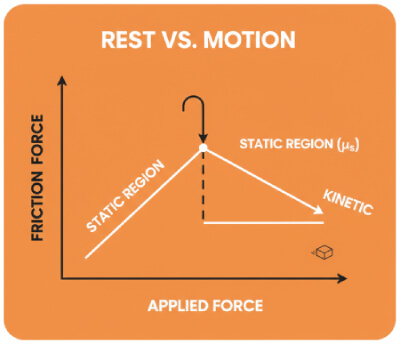
Seleccione el estado de movimiento (estático o cinético).
-
Ingrese el coeficiente de fricción ($\mu$) para su par de materiales.
-
Ingrese la masa del objeto ($m$) y el ángulo de inclinación de la superficie ($\theta$).
-
Revise la fuerza de fricción calculada y la predicción de movimiento.
Errores a evitar ⚠️
- Confundir masa con peso; el peso es m \ g.
- Usar el coeficiente cinético para determinar si un objeto empieza a moverse en lugar del estático.
- Ingresar el peso como fuerza normal en superficies inclinadas sin la corrección $\cos(\theta)$.
- Suponiendo que la fricción depende del área de la superficie; en el modelo de Coulomb, no depende.
Aplicaciones Prácticas📊
Determinar si un objeto permanecerá estacionario o se deslizará por una superficie inclinada.
Estimar el coeficiente de fricción necesario para el frenado de vehículos o el análisis de agarre de neumáticos.
Analizar las fuerzas de deslizamiento en ensamblajes mecánicos, sistemas de transporte o manejo de materiales.
Resolver problemas de física universitaria que involucran diagramas de cuerpo libre y planos inclinados.