Reibungskraft Rechner
Berechnen Sie die Reibung mithilfe von Koeffizienten und Normalkraft.
Berechnungsschritte
Berechnungsbeispiele
📋Schritte zur Berechnung
-
Wählen Sie den Bewegungszustand (statisch oder kinetisch).
-
Geben Sie den Reibungskoeffizienten ($\mu$) für Ihre Materialpaarung ein.
-
Geben Sie die Masse ($m$) und den Neigungswinkel ($\theta$) ein.
-
Überprüfen Sie die berechnete Reibungskraft und die Bewegungsprognose.
Häufige Fehler ⚠️
- Verwechslung von Masse und Gewicht; Gewicht ist m \ g.
- Verwendung des kinetischen Koeffizienten anstelle des statischen Koeffizienten, um zu entscheiden, ob sich ein Objekt bewegt.
- Eingabe des Gewichts als Normalkraft auf geneigten Flächen ohne die Korrektur $\cos(\theta)$.
- Annahme, dass die Reibung von der Oberfläche abhängt; im Coulomb-Modell ist dies nicht der Fall.
Praktische Anwendungen📊
Bestimmung, ob eine Last auf einer Rampe stationär bleibt oder abrutscht.
Abschätzung des erforderlichen Reibungskoeffizienten für Bremsanlagen oder Reifenhaftung.
Analyse von Gleitkräften in mechanischen Baugruppen, Fördersystemen oder Materialtransporten.
Lösen von universitären Physikaufgaben mit Freikörperdiagrammen und schiefen Ebenen.
Fragen und Antworten
Was ist Reibungskraft und warum ist sie wichtig?
Die Reibungskraft wirkt der Relativbewegung zwischen zwei Kontaktflächen entgegen. Sie ist entscheidend für mechanische Stabilität, Bremswirkung und die Berechnung von Energieverlusten in der Technik.
Wie berechne ich die Reibungskraft?
Multiplizieren Sie den Reibungskoeffizienten mit der Normalkraft: $F = \mu \cdot N$. Für schiefe Ebenen gilt $N = m \cdot g \cdot \cos(\theta)$.
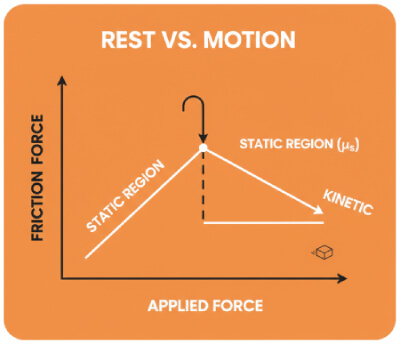
Was ist der Unterschied zwischen Haft- und Gleitreibung?
Die Haftreibung verhindert den Beginn der Bewegung bis zu einem Maximum von $\mu_s \cdot N$. Die Gleitreibung wirkt während des Rutschens mit einem konstanten Wert $\mu_k \cdot N$, der meist niedriger ist als die maximale Haftreibung.
Wie finde ich den Reibungskoeffizienten für verschiedene Materialien?
Koeffizienten werden experimentell ermittelt. Typische Werte liegen zwischen $0.05$ (Eis) und über $1.0$ (High-Grip-Gummi). Diese Werte finden Sie in Material-Tabellenbüchern.
Hängt die Reibung von der Oberflächengröße ab?
Nach den Amontons-Coulomb-Gesetzen ist die Reibung unabhängig von der scheinbaren Kontaktfläche. Sie hängt nur von der Materialbeschaffenheit und der Normalkraft ab.
Welche Formel nutzt dieser Reibungskraft-Rechner?
Unser Tool nutzt das klassische Modell der Festkörperreibung: $F_k = \mu_k \cdot N$ für kinetische und $F_s \leq \mu_s \cdot N$ für statische Fälle. Bei Neigungen wird $N = m \cdot g \cdot \cos(\theta)$ angewendet, was dem globalen Standard in Physik und Technik entspricht.
Hinweis: Dieser Rechner dient dazu, hilfreiche Schätzungen zu Informationszwecken bereitzustellen. Obwohl wir uns um Genauigkeit bemühen, können die Ergebnisse je nach örtlichen Gesetzen und individuellen Umständen variieren. Wir empfehlen, bei wichtigen Entscheidungen einen professionellen Berater zu Rate zu ziehen.