Friction Force Calculator

Calculate static or kinetic friction force on flat or inclined surfaces using the coefficient of friction and normal force.

Calculation Steps

Was this calculator helpful?

★ ★ ★ ★ ★
4.6/5 (16 votes)

Calculation Examples

Calculation Case Result
Steel on steel, static coefficient 0.74, 20 kg on flat surface Maximum static friction approx. 145 N
Rubber on concrete, kinetic coefficient 0.30, 50 kg on 25 degree incline Kinetic friction approx. 133 N, object slides
Wood on wood, static coefficient 0.60, 15 kg on 30 degree incline Maximum static friction approx. 76 N, object stays at rest

How to Use the Friction Force Calculator

Select the friction type first: static (object at rest) or kinetic (object already sliding). The coefficient of friction \(\mu\) differs between these two states for the same material pair, so choosing the correct type matters before entering any numbers.

Enter the coefficient of friction \(\mu\) for your material combination. If you do not know the value, standard engineering tables list coefficients for common pairs such as steel on steel, rubber on concrete, or wood on wood. Then provide either the normal force \(N\) in Newtons directly, or the object mass \(m\) in kilograms and the surface incline angle \(\theta\) in degrees. The calculator derives the normal force automatically: \(N = mg\cos\theta\) for inclined surfaces and \(N = mg\) for horizontal ones. It then computes the friction force and compares it against the gravitational component \(mg\sin\theta\) to predict whether the object will remain stationary or begin sliding.

The Physics of Friction: Formulas and Principles

Dry friction between solid surfaces is described by the Amontons-Coulomb model. The core relationship is: \[F_f = \mu \cdot N\]

Static friction acts as a self-adjusting resistive force that matches the applied force up to a maximum threshold: \[F_{s,\max} = \mu_s \cdot N\] When the applied force exceeds this threshold, motion begins. Once sliding starts, friction drops to the kinetic value: \[F_k = \mu_k \cdot N\] In nearly all material pairs, \(\mu_s > \mu_k\), which is why more force is needed to start an object moving than to keep it sliding. This difference is what makes anti-lock braking systems effective: keeping wheels rolling (static friction) produces more stopping force than locked wheels skidding (kinetic friction).

On an inclined plane at angle \(\theta\), the normal force is the perpendicular component of gravity: \[N = m \cdot g \cdot \cos\theta\] The gravitational component driving the object down the slope is \(mg\sin\theta\). The object remains stationary as long as \(\mu_s \cdot mg\cos\theta \geq mg\sin\theta\), which simplifies to \(\mu_s \geq \tan\theta\).

Diagram comparing static and kinetic friction force on a block at rest versus sliding on a surface

Useful Tips 💡

  • The coefficient of friction depends on both materials in contact and the surface condition: rubber on dry asphalt gives roughly 0.7-0.8, while rubber on wet ice drops to around 0.1.
  • Always use the static coefficient when checking whether motion will start; switch to kinetic only after motion has begun.

📋Steps to Calculate

  1. Select the motion state: static (at rest) or kinetic (already sliding).

  2. Enter the coefficient of friction for your material pair.

  3. Enter the object mass and surface incline angle, or the normal force directly.

  4. Review the friction force result and the motion prediction.

Mistakes to Avoid ⚠️

  1. Entering weight (in Newtons) and mass (in kg) interchangeably: weight equals mass times g, and they are not the same quantity.
  2. Using the kinetic coefficient to determine whether an object starts moving: that decision always requires the static coefficient.
  3. Entering the full weight as the normal force on an inclined surface without applying the cosine correction, which overstates friction.
  4. Assuming friction increases with contact area: under the Amontons-Coulomb model, friction force is independent of apparent contact area.

Practical Applications📊

  1. Determine whether an object will remain stationary or slide down an inclined surface given the friction coefficient and angle.

  2. Estimate the required friction coefficient for vehicle braking and tire grip under different road conditions.

  3. Analyze sliding forces in mechanical assemblies, conveyor belts, and material handling equipment.

Questions and Answers

What is friction force and why does it matter in engineering?

Friction force is the resistive force acting tangent to the contact interface between two surfaces, opposing relative motion or the tendency of motion. In mechanical engineering it plays both roles simultaneously: it is essential for braking, traction, fastener retention, and belt drives, while also being the primary source of energy loss and surface wear in rotating machinery. The American Society of Mechanical Engineers (ASME) estimates that roughly 20% of global energy consumption is lost to friction and the wear it causes, which is why accurate friction modeling is central to both design efficiency and maintenance planning.

How do I calculate friction force on an inclined surface?

On a slope at angle \(\theta\), the weight vector \(mg\) splits into two components. The component perpendicular to the surface is \(N = mg\cos\theta\), which determines the normal force and therefore the friction ceiling. The component parallel to the surface is \(mg\sin\theta\), which is the force trying to slide the object downhill. The maximum static friction that resists sliding is \(F_{s,\max} = \mu_s \cdot mg\cos\theta\). If \(\mu_s \cdot mg\cos\theta < mg\sin\theta\), equivalently if \(\mu_s < \tan\theta\), the object slides. This condition is the standard stability criterion taught in undergraduate statics courses.

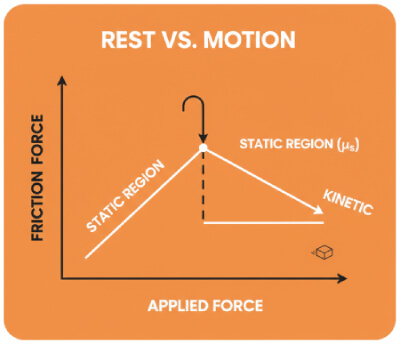
What is the difference between static and kinetic friction?

Static friction prevents relative motion between surfaces in contact. It is self-adjusting: it matches the applied force exactly until it reaches its maximum value \(F_{s,\max} = \mu_s \cdot N\), at which point the object starts moving. Kinetic friction acts once sliding has already begun and takes the fixed value \(F_k = \mu_k \cdot N\). Because \(\mu_s > \mu_k\) for virtually all material pairs, the transition from static to kinetic friction produces a sudden drop in resistive force, which is the physical reason objects tend to jerk or lurch when they first start sliding.

How are friction coefficients determined for different materials?

Friction coefficients are empirical values measured in controlled laboratory tests, typically by sliding one material over another under a known normal load and measuring the tangential force. Standard reference values appear in engineering handbooks such as Machinery's Handbook and the ASME standards for tribology. Common examples: dry steel on steel has \(\mu_s \approx 0.74\) and \(\mu_k \approx 0.42\); rubber on dry concrete ranges from 0.6 to 0.8; PTFE (Teflon) on steel is as low as 0.04, which is why it is used in low-friction bearings and non-stick surfaces.

Does contact surface area affect friction force?

Under the Amontons-Coulomb model of dry friction, the macroscopic contact area has no effect on friction force. The friction force depends only on the normal force and the coefficient, not on how large the touching surfaces are. This is counterintuitive but well-supported: a wide brake pad and a narrow one made of the same material provide the same friction force under the same normal load. The physical explanation is that real contact occurs only at microscopic asperities, and increasing apparent area spreads the same total load over more asperities without changing the total contact force.

What standards govern the friction model used in this calculator?

The calculator implements the classical Amontons-Coulomb model of dry friction: \(F_f = \mu N\) for kinetic friction and \(F_f \leq \mu_s N\) for static equilibrium. This model is the foundation of rigid-body mechanics as described in ISO 4287 (surface texture) and referenced in NIST technical documentation on tribology. For inclined surfaces, the normal force calculation follows Newton's second law applied to the perpendicular direction. The model is exact for idealized dry contacts and provides engineering-grade accuracy for most practical applications involving solid materials under moderate loads and speeds.

🔢Try More Calculators

Free Fall Calculator
Net Force Calculator
Potential Energy Calculator
Disclaimer: This calculator is designed to provide helpful estimates for informational purposes. While we strive for accuracy, financial (or medical) results can vary based on local laws and individual circumstances. We recommend consulting with a professional advisor for critical decisions.